What's 2 1 2 As A Decimal
Kalali
Mar 29, 2025 · 5 min read
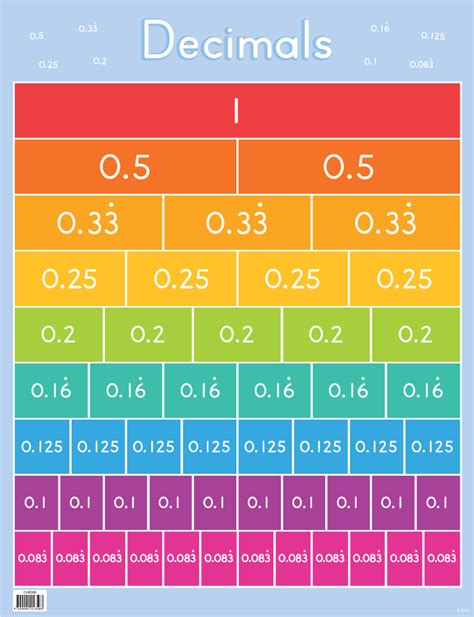
Table of Contents
What's 2 1/2 as a Decimal? A Comprehensive Guide
The question, "What's 2 1/2 as a decimal?" might seem simple at first glance. However, understanding the underlying concepts and various methods to solve this type of problem is crucial for anyone looking to improve their math skills and grasp fundamental numerical representations. This comprehensive guide will not only answer the question directly but also explore the broader context of converting fractions to decimals, offering diverse approaches and highlighting practical applications.
Understanding Fractions and Decimals
Before diving into the conversion, let's solidify our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator. This means we have one part out of two equal parts.
A decimal, on the other hand, represents a number using a base-ten system. The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions of a whole, in powers of ten (tenths, hundredths, thousandths, etc.). For example, 0.5 represents five-tenths (5/10), and 0.75 represents seventy-five hundredths (75/100).
Converting 2 1/2 to a Decimal: The Direct Approach
The mixed number 2 1/2 means two whole units and one-half of another unit. To convert this to a decimal, we first address the fractional part. We know that 1/2 is equivalent to 0.5. Therefore, 2 1/2 can be written as 2 + 0.5 = 2.5. This is the most straightforward and intuitive method.
Method 1: Converting the Fraction to a Decimal Directly
This method involves directly converting the fractional part of the mixed number into its decimal equivalent. Since we're dealing with 2 1/2, we focus on the fraction 1/2. To convert a fraction to a decimal, we divide the numerator by the denominator:
1 ÷ 2 = 0.5
Then, we add this decimal equivalent to the whole number part:
2 + 0.5 = 2.5
This method reinforces the fundamental operation of division in the context of fraction-to-decimal conversions.
Method 2: Using Equivalent Fractions
Another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This makes the conversion to a decimal much easier. In the case of 1/2, we can multiply both the numerator and denominator by 5 to get an equivalent fraction with a denominator of 10:
(1 × 5) / (2 × 5) = 5/10
Since 5/10 is equivalent to 0.5, we again arrive at:
2 + 0.5 = 2.5
This method enhances understanding of equivalent fractions and demonstrates a valuable technique for converting fractions with denominators that aren't easily divisible into powers of 10.
Method 3: Using Long Division
For more complex fractions, long division offers a systematic approach. While less efficient for simple fractions like 1/2, it's a valuable skill to master. To convert 1/2 to a decimal using long division, we divide 1 by 2:
0.5
2 | 1.0
1.0
---
0
This confirms that 1/2 = 0.5, leading us again to the final answer of 2.5. This method is especially useful when dealing with fractions that don't easily convert to equivalent fractions with denominators that are powers of 10.
Extending the Concept: Converting Other Mixed Numbers to Decimals
The techniques discussed above can be applied to convert any mixed number to a decimal. Let's consider a few examples:
- 3 1/4: 1/4 = 0.25 (either by division or recognizing that 1/4 = 25/100), so 3 1/4 = 3 + 0.25 = 3.25
- 1 3/5: 3/5 = 0.6 (multiplying numerator and denominator by 2 to get 6/10), so 1 3/5 = 1 + 0.6 = 1.6
- 4 7/8: 7/8 = 0.875 (long division is most straightforward here), so 4 7/8 = 4 + 0.875 = 4.875
These examples demonstrate the versatility of the methods described, enabling the conversion of a wide range of mixed numbers to their decimal equivalents.
Practical Applications of Decimal Conversions
Understanding how to convert fractions to decimals is essential in various real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins often requires converting fractions to decimals.
- Engineering: Precise measurements and calculations in engineering rely on decimal representations.
- Science: Scientific data frequently involves decimal numbers, making conversion from fractions crucial for analysis.
- Cooking and Baking: Recipe measurements often involve fractions, but using decimal equivalents in calculations can lead to more accurate results.
- Everyday Calculations: Many daily calculations, from splitting bills to calculating distances, can benefit from the ease of decimal arithmetic.
Mastering fraction-to-decimal conversion skills empowers individuals to tackle a wider range of numerical problems with confidence and precision.
Beyond the Basics: Repeating Decimals
It's important to note that not all fractions result in terminating decimals (decimals that end). Some fractions produce repeating decimals, where a sequence of digits repeats infinitely. For example, 1/3 = 0.3333... (the 3 repeats indefinitely). These are usually represented with a bar over the repeating digit(s), like this: 0.<u>3</u>. Understanding repeating decimals is important for more advanced mathematical operations.
Conclusion: Mastering Decimal Conversions
Converting 2 1/2 to a decimal, resulting in 2.5, is a straightforward process that exemplifies the fundamental principles of fraction-to-decimal conversions. This seemingly simple task opens doors to a broader understanding of numerical representations and their practical applications in various fields. Through mastering different methods—direct conversion, equivalent fractions, and long division—individuals gain a versatile skillset, facilitating efficient and accurate calculations across diverse scenarios. By understanding both terminating and repeating decimals, one achieves a more complete grasp of the numerical world, paving the way for more advanced mathematical pursuits. The ability to confidently navigate these conversions is a valuable asset in both academic and professional contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's 2 1 2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
