Whats 3 To The Power Of 3
Kalali
Apr 25, 2025 · 5 min read
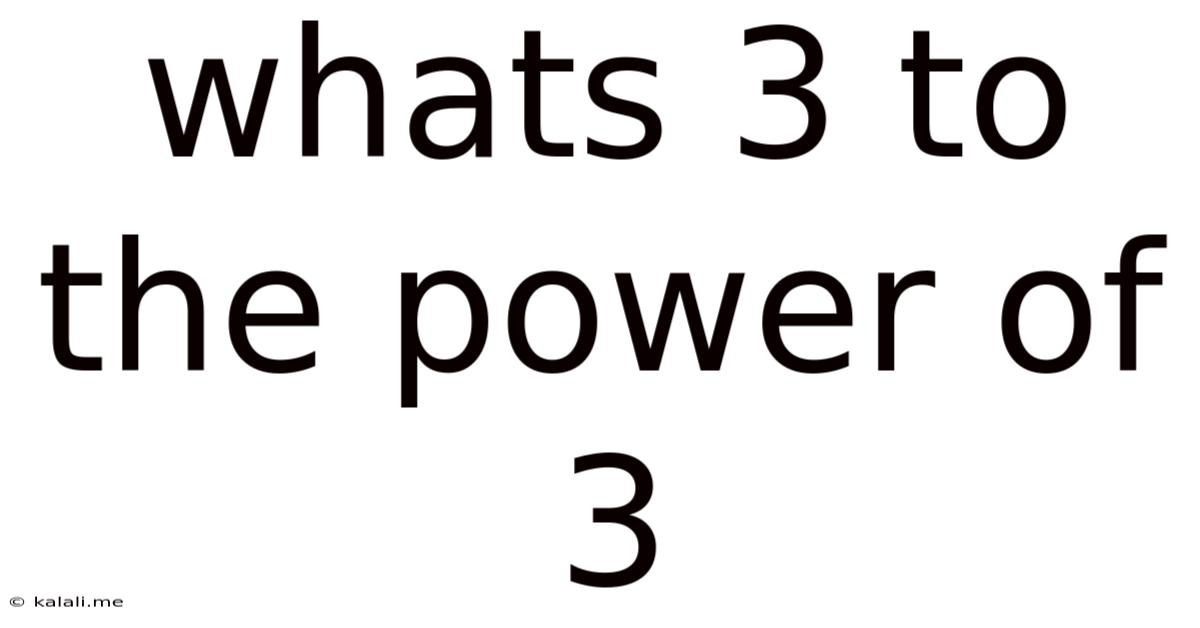
Table of Contents
What's 3 to the Power of 3? A Deep Dive into Exponentiation and its Applications
What is 3 to the power of 3? The simple answer is 27. But this seemingly straightforward mathematical calculation opens the door to a fascinating exploration of exponentiation, its properties, its prevalence in various fields, and its implications in more complex mathematical concepts. This article will delve deep into the meaning of 3³, exploring its fundamental principles, practical applications, and related mathematical concepts. We'll move beyond the basic calculation and uncover the rich tapestry woven by this seemingly simple equation.
Understanding Exponentiation: The Basics
Exponentiation, often represented by a superscript number (the exponent), indicates repeated multiplication. In the expression 3³, the base is 3 and the exponent is 3. This means we multiply the base (3) by itself the number of times specified by the exponent (3): 3 x 3 x 3 = 27. This seemingly simple operation forms the foundation of many advanced mathematical concepts.
Understanding exponentiation is crucial because it permeates numerous areas, from simple calculations to complex scientific models. This concept allows us to express extremely large or extremely small numbers concisely, making it a powerful tool in various disciplines.
Beyond 3³: Exploring Different Bases and Exponents
While 3³ provides a clear example, the concept of exponentiation extends far beyond this specific calculation. Let's consider other examples to illustrate its versatility:
-
2⁵ (2 to the power of 5): This means 2 x 2 x 2 x 2 x 2 = 32. This simple calculation is essential in understanding binary systems, the foundation of computer science.
-
10⁴ (10 to the power of 4): This equals 10,000 and demonstrates how exponents can quickly generate large numbers, crucial for understanding scientific notation and large-scale data.
-
5⁰ (5 to the power of 0): Any non-zero number raised to the power of 0 equals 1. This seemingly counterintuitive rule is a fundamental property of exponents.
-
4⁻² (4 to the power of -2): Negative exponents represent reciprocals. This equals 1/4² = 1/16. This is crucial in understanding scientific notation for extremely small numbers.
Applications of Exponentiation Across Disciplines
The seemingly simple calculation of 3³ has far-reaching implications across various fields. Let's examine some of them:
1. Computer Science and Binary Systems
Exponentiation is fundamental to computer science, specifically in binary systems (base-2). Every number in a computer is represented using a series of 0s and 1s. Understanding powers of 2 is crucial for calculating memory size, data transfer rates, and algorithm efficiency. For example, 2¹⁰ (1024) is approximately 1 kilobyte, a common unit of data storage.
2. Financial Mathematics and Compound Interest
Exponentiation plays a critical role in compound interest calculations. The formula for compound interest involves exponential growth, where the principal amount increases exponentially over time. Understanding exponentiation helps predict the future value of investments and assess the impact of different interest rates.
3. Physics and Engineering
Exponentiation is crucial in various physics and engineering applications. For example, exponential decay describes the decrease in radioactive material over time, while exponential growth models population increase or the spread of infectious diseases. Understanding these exponential models is critical for predicting and managing various phenomena.
4. Biology and Population Growth
Exponential functions are frequently used to model population growth in biology. The rate of population growth often follows an exponential pattern, particularly in environments with abundant resources. Understanding this growth pattern allows biologists to predict future population sizes and analyze ecological dynamics.
5. Chemistry and Chemical Reactions
Exponentiation appears in chemical reaction rates. Some reactions exhibit exponential kinetics, where the reaction rate is exponentially related to the concentration of reactants. This understanding is crucial for controlling and optimizing chemical processes.
Mathematical Concepts Related to Exponentiation
Understanding 3³ opens doors to comprehending more complex mathematical concepts:
1. Logarithms
Logarithms are the inverse of exponentiation. If 3³ = 27, then the logarithm base 3 of 27 is 3 (log₃27 = 3). Logarithms are crucial for solving exponential equations and are used extensively in various scientific and engineering calculations.
2. Exponential Functions
An exponential function is a function where the independent variable (x) appears in the exponent. A typical example is f(x) = aˣ, where 'a' is a constant. These functions describe exponential growth and decay phenomena observed in various natural processes.
3. Polynomial Functions
While not directly related to exponentiation in the same way logarithms are, understanding exponentiation helps understand polynomials. Polynomials are sums of terms involving variables raised to non-negative integer powers (exponents). For instance, x² + 3x + 2 is a polynomial where x is raised to the power of 2 and 1. The exponents determine the degree and behavior of the polynomial.
4. Complex Numbers
Exponentiation can be extended to complex numbers, where the base and/or exponent can be complex numbers. Euler's formula, e^(ix) = cos(x) + i sin(x), beautifully connects exponentiation with trigonometric functions and forms the foundation of many advanced mathematical concepts.
3³ in Everyday Life: Unexpected Applications
While seemingly abstract, the concept of 3³ surfaces in unexpected ways in our daily lives. Consider these examples:
-
Volume Calculations: Imagine a cube with sides of 3 units. The volume is 3 x 3 x 3 = 27 cubic units. This simple calculation illustrates the practical application of exponentiation in geometry.
-
Game Design: In many games, power-ups or upgrades might follow an exponential scaling pattern. For instance, the effect of a certain item might increase by a factor of 3³ as the player progresses.
-
Data Representation: The size of a data structure in computer programming might be based on powers of 3, although less common than powers of 2.
Conclusion: The Significance of a Simple Calculation
While the answer to "What's 3 to the power of 3?" is simply 27, this seemingly simple calculation unlocks a vast and intricate world of mathematical concepts and their practical applications. From understanding binary systems in computer science to modeling population growth in biology and calculating compound interest in finance, exponentiation is an indispensable tool across numerous disciplines. Its exploration reveals the interconnectedness of seemingly disparate fields and highlights the power of fundamental mathematical principles in shaping our understanding of the world around us. The seemingly simple 27 is a gateway to a much larger, fascinating mathematical universe.
Latest Posts
Latest Posts
-
What Is 11 Out Of 16
Apr 26, 2025
-
One Percent Of A Million Dollars
Apr 26, 2025
-
How Much Is 240ml In Cups
Apr 26, 2025
-
How Many Feet Are In 50 In
Apr 26, 2025
-
250 Ml Of Water To Cups
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about Whats 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.