Whats The Greatest Common Factor Of 24 And 36
Kalali
Aug 01, 2025 · 6 min read
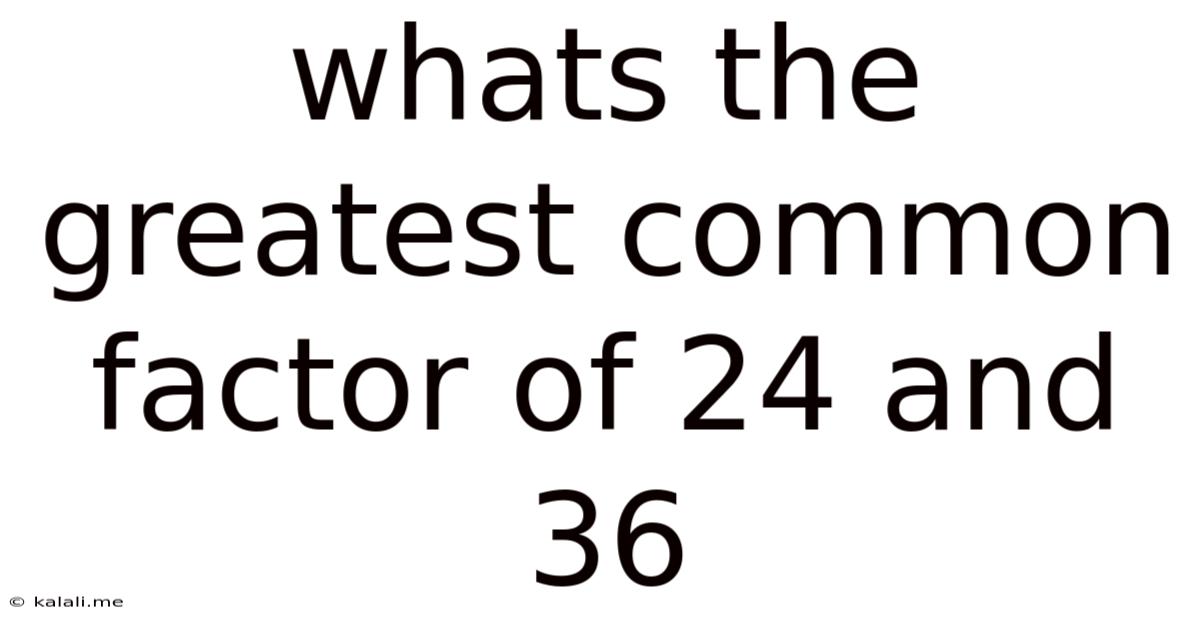
Table of Contents
Unveiling the Greatest Common Factor: A Deep Dive into 24 and 36
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic exercise, but understanding the underlying concepts unlocks a world of mathematical possibilities. This article will not only reveal the GCF of 24 and 36 but also explore various methods to find it, delve into the significance of GCF in different mathematical contexts, and examine its practical applications in everyday life. This comprehensive guide aims to provide a complete understanding of GCF, exceeding the typical explanation and serving as a valuable resource for students, teachers, and anyone curious about number theory.
What is the Greatest Common Factor (GCF)?
The greatest common factor, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For instance, if we consider the numbers 12 and 18, the GCF is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding this fundamental concept is crucial for various mathematical operations and problem-solving.
Finding the GCF of 24 and 36: Multiple Approaches
Now, let's tackle the specific question: What is the greatest common factor of 24 and 36? We can employ several methods to find the GCF, each offering a unique perspective on this mathematical concept.
1. Prime Factorization Method:
This method involves breaking down each number into its prime factors – prime numbers that multiply together to give the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 36: 36 = 2 x 2 x 3 x 3 = 2² x 3²
Once we have the prime factorization, we identify the common prime factors and their lowest powers. In this case, both 24 and 36 share 2 and 3 as prime factors. The lowest power of 2 is 2² (or 4) and the lowest power of 3 is 3¹ (or 3). Therefore, the GCF is the product of these common prime factors raised to their lowest powers:
GCF(24, 36) = 2² x 3¹ = 4 x 3 = 12
2. Listing Factors Method:
This is a more straightforward, albeit less efficient method, particularly for larger numbers. We list all the factors (numbers that divide evenly) of each number and then identify the largest factor common to both lists.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Comparing the two lists, we see that the common factors are 1, 2, 3, 4, 6, and 12. The greatest of these common factors is 12. Therefore, GCF(24, 36) = 12.
3. Euclidean Algorithm:
This method is particularly efficient for larger numbers and is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
- Start with the two numbers: 36 and 24.
- Subtract the smaller number from the larger number: 36 - 24 = 12
- Replace the larger number with the difference: The new pair is 24 and 12.
- Repeat: 24 - 12 = 12. The new pair is 12 and 12.
- Since the numbers are now equal, the GCF is 12.
Therefore, GCF(24, 36) = 12.
The Significance of GCF in Mathematics
The concept of GCF extends far beyond simple arithmetic. It plays a crucial role in various mathematical areas, including:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 24/36 can be simplified by dividing both the numerator and the denominator by their GCF (12), resulting in the simplified fraction 2/3.
-
Solving Equations: GCF is sometimes used in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Number Theory: GCF is a fundamental concept in number theory, a branch of mathematics concerned with the properties of integers. It's used in many advanced theorems and proofs.
-
Modular Arithmetic: GCF is essential in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). This has applications in cryptography and computer science.
Real-World Applications of GCF
The GCF is not just a theoretical concept; it has practical applications in everyday life:
-
Dividing Objects: Imagine you have 24 apples and 36 oranges, and you want to divide them into equal groups, with each group containing the same number of apples and oranges. The GCF (12) tells you that you can create 12 equal groups, each containing 2 apples and 3 oranges.
-
Measurement and Construction: In construction or carpentry, determining the GCF can help in cutting materials efficiently. For example, if you have two pieces of wood measuring 24 inches and 36 inches, finding the GCF (12) would allow you to cut both pieces into equal lengths of 12 inches without any waste.
-
Scheduling and Time Management: The GCF can be useful in scheduling tasks or events that occur at different intervals. For example, if event A happens every 24 days and event B happens every 36 days, the GCF (12) indicates that both events will coincide every 12 days.
-
Pattern Recognition: In various fields like music, art, and design, understanding GCF could help in recognizing and creating repeating patterns and rhythmic sequences.
Extending the Concept: Least Common Multiple (LCM)
While this article focuses on the GCF, it's important to mention the closely related concept of the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of each of the integers. The relationship between GCF and LCM is given by the formula:
LCM(a, b) = (a x b) / GCF(a, b)
For our example of 24 and 36, the LCM is (24 x 36) / 12 = 72.
Conclusion: Mastering the GCF and Beyond
Understanding the greatest common factor is a cornerstone of mathematical literacy. From simplifying fractions to solving complex equations and even managing everyday tasks, the GCF proves its versatility and importance. Through different methods like prime factorization, listing factors, and the Euclidean algorithm, we can efficiently determine the GCF of any two numbers. This knowledge provides a solid foundation for further exploration into more advanced mathematical concepts and problem-solving techniques. The journey into the world of number theory, ignited by the seemingly simple question of finding the GCF of 24 and 36, is a testament to the beauty and practicality of mathematics. Remember, the ability to find the GCF isn’t just about getting the right answer; it’s about understanding the process and applying it effectively to various scenarios. This comprehensive analysis of GCF will equip you with the knowledge and skills needed to confidently tackle related problems and appreciate the significance of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
How Many Tablespoons Are In A Packet Of Ranch Seasoning
Aug 03, 2025
-
How Many Minutes Are In 360 Seconds
Aug 03, 2025
-
How To Calculate Square Feet Into Linear Feet
Aug 03, 2025
-
What Is A 56 Out Of 60
Aug 03, 2025
-
How Long Does Brandy Melville Take To Ship
Aug 03, 2025
Related Post
Thank you for visiting our website which covers about Whats The Greatest Common Factor Of 24 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.