What's The Square Root Of 244
Kalali
Mar 30, 2025 · 5 min read
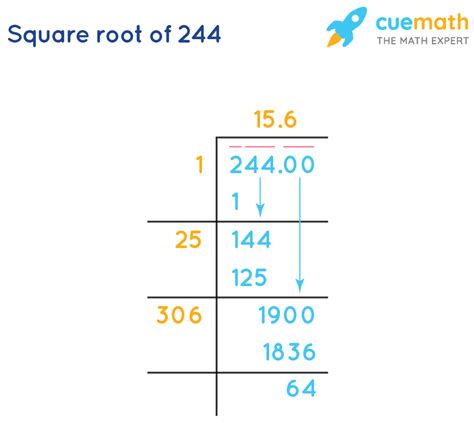
Table of Contents
Decoding the Square Root of 244: A Deep Dive into Methods and Applications
The seemingly simple question, "What's the square root of 244?", opens a door to a fascinating world of mathematical concepts and practical applications. While a calculator readily provides the decimal approximation (approximately 15.6205), understanding the process behind finding this value reveals deeper insights into number theory and its relevance across various fields. This article delves into different methods of calculating the square root of 244, exploring both the theoretical underpinnings and real-world uses.
Understanding Square Roots
Before we delve into the specifics of calculating the square root of 244, let's establish a foundational understanding of what a square root represents. The square root of a number, 'x', is a value that, when multiplied by itself (squared), equals 'x'. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 is 3 because 3 * 3 = 9.
The square root of 244, however, isn't a whole number. It's an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating. This is where the challenge and the intrigue lie.
Methods for Calculating √244
Several methods can be employed to calculate the square root of 244, each with its own level of complexity and accuracy. Let's explore some of the most common approaches:
1. Prime Factorization Method:
This method begins by finding the prime factorization of 244. Prime factorization involves breaking down a number into its prime number components (numbers divisible only by 1 and themselves).
244 = 2 x 2 x 61
Since 61 is a prime number, we cannot simplify the expression further. This prime factorization helps us understand the number's structure but doesn't directly give us the square root. We can, however, observe that there's no perfect square factor (a number that is the square of an integer) within the factorization, confirming that the square root of 244 is irrational.
2. The Babylonian Method (or Heron's Method):
This iterative method provides an increasingly accurate approximation of the square root. It involves starting with an initial guess and refining it through repeated calculations.
- Step 1: Initial Guess: Let's start with a guess of 15.
- Step 2: Iteration: The formula for the Babylonian method is: x_(n+1) = 0.5 * (x_n + 244/x_n), where x_n is the current guess and x_(n+1) is the next improved guess.
- Step 3: Repetition: We repeat step 2, using the new guess as the input for the next iteration. The more iterations performed, the closer the approximation will get to the actual value.
Let's do a few iterations:
- Iteration 1: x_1 = 0.5 * (15 + 244/15) ≈ 15.6333
- Iteration 2: x_2 = 0.5 * (15.6333 + 244/15.6333) ≈ 15.6205
As you can see, even after just two iterations, we've reached a highly accurate approximation of the square root of 244. Further iterations would yield even greater precision.
3. Using a Calculator or Computer Software:
The simplest and most practical method for obtaining the square root of 244 is by using a calculator or computer software with a built-in square root function. These tools utilize sophisticated algorithms to calculate the value to a high degree of accuracy. The result, as mentioned earlier, is approximately 15.6205.
4. Long Division Method:
A more manual, albeit less efficient approach, is the long division method for finding square roots. This method involves a series of steps involving subtracting multiples of the current digit, similar to long division, but more involved. While feasible, it's generally less favored due to its complexity and time-consuming nature compared to other methods.
Applications of Square Roots
The concept of square roots, though seemingly abstract, finds wide application in numerous fields:
1. Geometry and Trigonometry: Square roots are fundamental in calculating distances, areas, and volumes. For instance, determining the length of the diagonal of a rectangle or the hypotenuse of a right-angled triangle involves applying the Pythagorean theorem, which inherently uses square roots.
2. Physics: Many physical phenomena involve square roots. For example, calculations related to velocity, acceleration, and energy frequently utilize square roots. Calculating the velocity of a falling object, for instance, uses the square root of the distance fallen.
3. Engineering and Architecture: Square roots play a crucial role in structural design and calculations. In designing buildings, bridges, and other structures, engineers use square roots to determine load-bearing capacity, stress, and strain on materials.
4. Statistics: Standard deviation, a crucial measure of data dispersion, involves calculating the square root of the variance. This is essential for understanding the spread of data around the mean.
5. Computer Graphics and Game Development: Square roots are extensively used in calculating distances between points in two or three-dimensional space, which is fundamental in rendering graphics, handling physics simulations, and creating realistic game environments.
6. Finance: Square roots appear in financial calculations such as determining portfolio risk (standard deviation of returns) and options pricing models.
7. Signal Processing: In signal processing, square roots are used in computing the magnitude of complex numbers, essential in analyzing signals and images.
Beyond the Calculation: Exploring Irrational Numbers
The square root of 244's irrationality highlights a fascinating aspect of mathematics: the existence of numbers that cannot be expressed as precise fractions. Irrational numbers, like π (pi) and e (Euler's number), have significant roles in various mathematical fields. Their infinite, non-repeating decimal representations highlight the richness and complexity within seemingly simple mathematical concepts. Understanding these numbers' properties and behavior is crucial to advancing our understanding of mathematics as a whole.
Conclusion
Finding the square root of 244, initially a simple numerical problem, opens up a world of mathematical exploration. While a calculator provides the approximate decimal answer quickly, the journey to understanding the different calculation methods reveals fundamental concepts in number theory, algebra, and iterative processes. Furthermore, the applications of square roots span a wide spectrum of disciplines, showcasing their practical significance in fields ranging from engineering and physics to finance and computer graphics. This exploration underscores the interconnectedness of seemingly disparate mathematical concepts and their powerful impact on our understanding and manipulation of the world around us. Therefore, the seemingly simple question, "What's the square root of 244?", serves as a powerful starting point for a deeper appreciation of the beauty and utility of mathematics.
Latest Posts
Latest Posts
-
How Many Gallons Is 7 Litres
Apr 01, 2025
-
160 Degrees Celsius Is What In Fahrenheit
Apr 01, 2025
-
62 C Is What In F
Apr 01, 2025
-
Which Type Of Mutation Stops The Translation Of Mrna
Apr 01, 2025
-
500 Mg Is Equal To How Many Grams
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 244 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
