Whats The Square Root Of -4
Kalali
Apr 24, 2025 · 5 min read
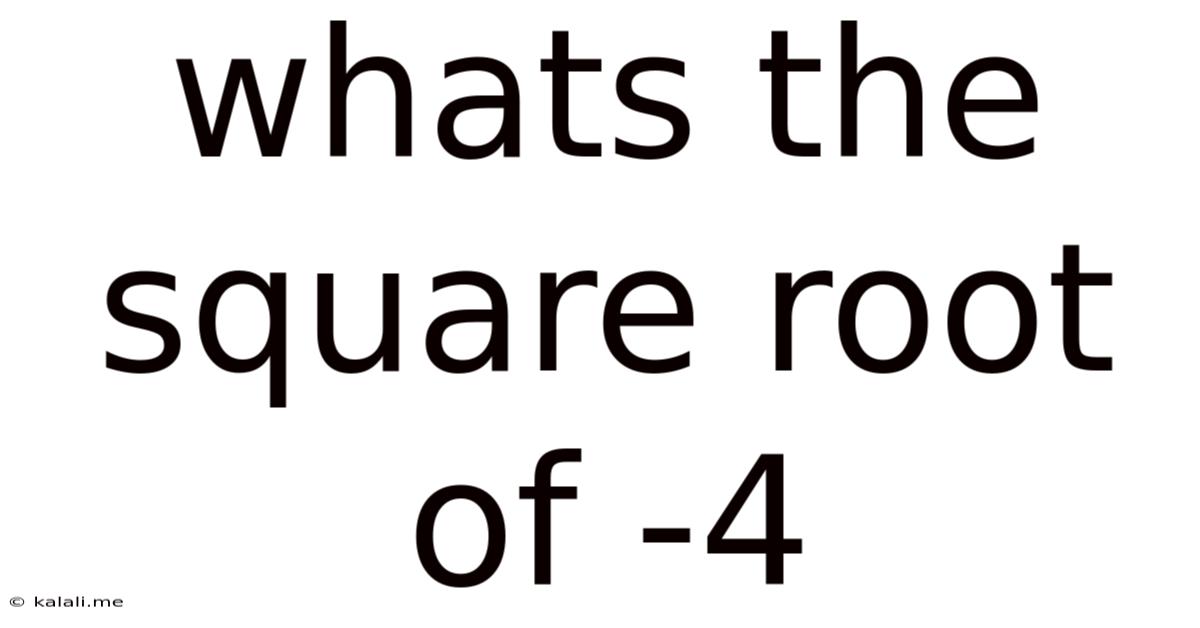
Table of Contents
What's the Square Root of -4? Delving into the Realm of Imaginary Numbers
The question, "What's the square root of -4?" might seem simple at first glance. After all, finding the square root of a number is a fundamental mathematical operation. However, this seemingly straightforward question leads us down a fascinating path into the world of complex numbers, specifically the realm of imaginary numbers. This article will explore the concept of the square root of negative numbers, explain the mathematical background behind imaginary units, and demonstrate practical applications of this concept in various fields. Understanding this concept is crucial for anyone pursuing advanced mathematics, physics, or engineering.
What Makes -4 Different?
The square root of a number, denoted as √x, is the value that, when multiplied by itself, equals x. For example, √9 = 3 because 3 * 3 = 9. Similarly, √16 = 4 because 4 * 4 = 16. The challenge arises when we try to find the square root of a negative number. No real number, when multiplied by itself, can produce a negative result. This is because the product of two positive numbers is positive, and the product of two negative numbers is also positive. This limitation necessitates the introduction of a new type of number: the imaginary number.
Introducing the Imaginary Unit: 'i'
To address the problem of finding the square root of negative numbers, mathematicians defined the imaginary unit, denoted by the letter 'i', as follows:
i = √-1
This definition might seem arbitrary, but it provides a consistent and logical framework for working with negative square roots. It's crucial to remember that 'i' is not a real number; it exists in a separate number system.
Calculating the Square Root of -4
Now, let's tackle the original question: What's the square root of -4? Using the definition of the imaginary unit, we can rewrite √-4 as follows:
√-4 = √(4 * -1) = √4 * √-1 = 2 * i = 2i
Therefore, the square root of -4 is 2i. It's important to note that, unlike real numbers, imaginary numbers have both a magnitude and a direction (represented by the positive or negative sign).
Expanding to Complex Numbers
Imaginary numbers rarely stand alone; they usually combine with real numbers to form complex numbers. A complex number is a number that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. 'a' is called the real part, and 'b' is called the imaginary part.
For instance, 3 + 2i is a complex number where the real part is 3 and the imaginary part is 2. Similarly, -1 – 5i is another example, with a real part of -1 and an imaginary part of -5. Complex numbers provide a comprehensive number system that encompasses both real and imaginary numbers.
Understanding the Geometry of Complex Numbers: The Complex Plane
Visualizing complex numbers is crucial for comprehending their properties. The complex plane, also known as the Argand plane, is a two-dimensional graphical representation where the horizontal axis (x-axis) represents the real part and the vertical axis (y-axis) represents the imaginary part. Each complex number can be plotted as a point on this plane.
For instance, the complex number 3 + 2i would be plotted at the point (3, 2) on the complex plane. This graphical representation helps in understanding operations on complex numbers, such as addition, subtraction, multiplication, and division, which involve vector operations on the complex plane.
Operations with Complex Numbers
Performing arithmetic operations on complex numbers involves treating the real and imaginary parts separately.
-
Addition and Subtraction: Add or subtract the real parts and the imaginary parts separately. For example: (3 + 2i) + (1 - i) = (3 + 1) + (2 - 1)i = 4 + i
-
Multiplication: Use the distributive property (FOIL method) and remember that i² = -1. For example: (2 + i)(3 - 2i) = 2(3) + 2(-2i) + i(3) + i(-2i) = 6 - 4i + 3i - 2i² = 6 - i + 2 = 8 - i
-
Division: Multiply both the numerator and denominator by the complex conjugate of the denominator. The complex conjugate of a + bi is a - bi. For example: (1 + i) / (2 - i) = (1 + i)(2 + i) / (2 - i)(2 + i) = (2 + i + 2i + i²) / (4 - i²) = (2 + 3i - 1) / (4 + 1) = (1 + 3i) / 5 = 1/5 + (3/5)i
Applications of Imaginary and Complex Numbers
While the concept of imaginary numbers might seem abstract, they have significant practical applications across various fields:
-
Electrical Engineering: Complex numbers are fundamental in analyzing alternating current (AC) circuits. They simplify calculations involving impedance, voltage, and current, which are crucial for designing and troubleshooting electrical systems. Imaginary numbers represent the reactive components (inductors and capacitors) in the circuit.
-
Quantum Mechanics: Complex numbers are integral to the mathematical framework of quantum mechanics. Wave functions, which describe the state of a quantum system, are often complex-valued functions. The probabilities associated with quantum events are calculated using the magnitudes of these wave functions.
-
Signal Processing: In signal processing, complex numbers are used to represent signals in the frequency domain using the Fourier transform. This allows for efficient signal analysis, filtering, and manipulation, with applications in areas like audio processing, image processing, and telecommunications.
-
Fluid Dynamics: Complex numbers find application in solving certain types of fluid flow problems, especially those involving potential flow. The use of complex analysis simplifies calculations and provides elegant solutions.
Beyond the Square Root of -4: Exploring Higher Powers of 'i'
The powers of 'i' exhibit a cyclical pattern:
- i¹ = i
- i² = -1
- i³ = i² * i = -i
- i⁴ = i² * i² = (-1)(-1) = 1
- i⁵ = i⁴ * i = 1 * i = i
- i⁶ = i⁴ * i² = 1 * (-1) = -1
This pattern repeats every four powers. This cyclical nature simplifies calculations involving higher powers of 'i'.
Conclusion: The Importance of Imaginary Numbers
The seemingly simple question, "What's the square root of -4?", has led us on a journey into the fascinating world of imaginary and complex numbers. These numbers, while initially abstract, are essential tools in various scientific and engineering disciplines. Their applications demonstrate the power and elegance of extending mathematical concepts beyond the limitations of real numbers. Understanding imaginary and complex numbers is a pivotal step in advancing mathematical proficiency and tackling problems in diverse fields. It shows how mathematics evolves to address challenges and provides powerful tools for solving complex problems in the real world, proving that even seemingly paradoxical concepts like the square root of a negative number hold immense practical significance.
Latest Posts
Latest Posts
-
4 M Equals How Many Feet
Apr 24, 2025
-
How Many Kilograms Is 50 Grams
Apr 24, 2025
-
2 5 Kg Is How Many Grams
Apr 24, 2025
-
34 Degrees Celsius Converted To Fahrenheit
Apr 24, 2025
-
What Processes Changed The Earths Environment During Precambrian Time
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of -4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.