When To Use Brackets Or Parentheses In Domain And Range
Kalali
Mar 28, 2025 · 5 min read
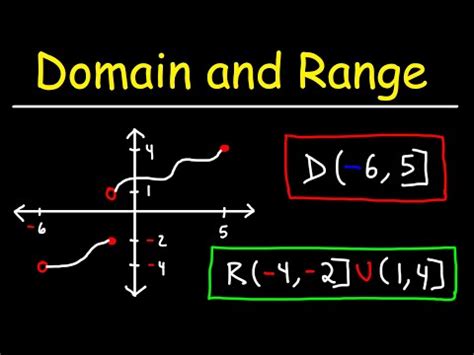
Table of Contents
When to Use Brackets or Parentheses in Domain and Range
Understanding the nuances of using brackets and parentheses when expressing the domain and range of a function is crucial for accurate mathematical communication. While seemingly minor, this notation significantly impacts the interpretation of the function's behavior at its boundaries. This comprehensive guide will delve into the precise use of these symbols, clarifying their meaning and providing numerous examples to solidify your understanding.
The Fundamentals: Open and Closed Intervals
Before diving into the specifics of domain and range, let's review the fundamental concepts of open and closed intervals. These intervals describe sets of numbers, and the use of parentheses and brackets directly reflects whether the endpoints are included or excluded.
-
Open Interval: Represented by parentheses
( ), an open interval indicates that the endpoints are not included in the set. For example,(2, 5)represents all numbers greater than 2 and less than 5, but not 2 or 5 themselves. -
Closed Interval: Represented by brackets
[ ], a closed interval indicates that the endpoints are included in the set. For example,[2, 5]represents all numbers greater than or equal to 2 and less than or equal to 5, including both 2 and 5. -
Half-Open Intervals: These intervals use a combination of parentheses and brackets, indicating that one endpoint is included while the other is excluded. For example:
[2, 5)includes 2 but excludes 5.(2, 5]excludes 2 but includes 5.
Applying Interval Notation to Domain and Range
The domain of a function represents all possible input values (x-values) for which the function is defined. The range represents all possible output values (y-values) that the function can produce. The choice between brackets and parentheses when describing these sets depends entirely on whether the endpoints are included.
Domain: Identifying Included and Excluded Values
Determining the domain often involves considering several factors:
-
Division by Zero: Functions with denominators must exclude any values of x that would make the denominator zero. For example, in the function f(x) = 1/(x-3), the domain is (-∞, 3) ∪ (3, ∞) because x cannot equal 3. Note the use of parentheses around 3 to indicate its exclusion.
-
Even Roots: Functions involving even roots (square roots, fourth roots, etc.) must restrict the input to non-negative values inside the root. For example, the domain of f(x) = √(x-4) is [4, ∞) because x-4 must be greater than or equal to zero. The bracket
[at 4 indicates that 4 is included in the domain (√0 = 0). -
Logarithms: Logarithmic functions are only defined for positive arguments. For example, the domain of f(x) = log(x+2) is (-2, ∞). Parentheses are used because the logarithm is undefined at x = -2.
-
Piecewise Functions: Piecewise functions are defined differently across different intervals. Careful attention to the defined intervals for each piece is needed when determining the overall domain. The domain will be the union of all the individual intervals.
Examples of Domain Notation:
- f(x) = x²: Domain: (-∞, ∞) (All real numbers)
- f(x) = 1/x: Domain: (-∞, 0) ∪ (0, ∞)
- f(x) = √x: Domain: [0, ∞)
- f(x) = √(9 - x²): Domain: [-3, 3]
- f(x) = { x+1 if x<0; x-1 if x>=0}: Domain: (-∞, ∞)
Range: Determining the Output Values
The range of a function is determined by analyzing the possible output values. This often involves considering the function's behavior as x approaches its domain boundaries and its overall shape. Graphing the function can be a helpful visual aid.
-
Bounded Functions: Functions with a maximum or minimum value will have a bounded range. For example, the range of f(x) = -x²+4 is (-∞, 4], as the maximum output is 4, and the function extends infinitely downwards. The bracket
]at 4 signifies its inclusion. -
Unbounded Functions: Functions that extend infinitely in one or both directions will have unbounded ranges. For example, the range of f(x) = x³ is (-∞, ∞).
-
Rational Functions: Analyzing the asymptotes and behavior of rational functions (ratios of polynomials) is crucial for determining the range. Sometimes the range might have gaps or be divided into intervals.
-
Trigonometric Functions: Trigonometric functions have cyclical ranges, often bounded by specific values like -1 and 1 (for sine and cosine).
Examples of Range Notation:
- f(x) = x²: Range: [0, ∞)
- f(x) = 1/x: Range: (-∞, 0) ∪ (0, ∞)
- f(x) = √x: Range: [0, ∞)
- f(x) = sin(x): Range: [-1, 1]
- f(x) = x³: Range: (-∞, ∞)
Common Mistakes and Clarifications
Several common mistakes occur when using brackets and parentheses in domain and range notation:
-
Confusing Open and Closed Intervals: Incorrectly using parentheses when brackets are required, or vice versa, leads to an inaccurate representation of the function's behavior at its boundaries.
-
Ignoring Asymptotes: For rational functions, failing to consider vertical or horizontal asymptotes can result in an incomplete or incorrect range.
-
Incorrect Union Notation: When the domain or range consists of disjoint intervals (separate sections), using the union symbol (∪) is crucial to correctly represent the entire set. Failing to do so will lead to an incomplete answer.
-
Inconsistent Notation: Mixing bracket and parentheses styles inconsistently within a single expression is confusing and should be avoided.
Advanced Considerations: Piecewise Functions and Other Complex Cases
Piecewise functions present a unique challenge. The domain of the entire piecewise function is the union of the domains of each piece. The range requires careful analysis of each piece's output and the potential overlap.
Furthermore, functions with more complex definitions, such as those involving absolute values or piecewise defined functions with discontinuous sections, require a meticulous examination to correctly determine the domain and range and accurately use the appropriate interval notation.
Conclusion: Precision in Mathematical Communication
The correct use of brackets and parentheses when describing the domain and range of a function is vital for clear and unambiguous mathematical communication. By carefully considering the function's behavior at its boundaries and using interval notation accurately, you can express mathematical concepts precisely and avoid potential misunderstandings. Remember to always double-check your work and consider graphing the function as a valuable tool to verify your findings. Mastering this notation is a key step in developing a strong understanding of functional analysis.
Latest Posts
Latest Posts
-
In What Episode Of Bleach Does Ichigo Ask Orihime Out
Jul 13, 2025
-
How Much Is 4 Oz Chocolate Chips
Jul 13, 2025
-
How Many Times Does 9 Go Into 70
Jul 13, 2025
-
4 Pics 1 Word Cheat 8 Letters
Jul 13, 2025
-
220 Kilometers Per Hour To Miles Per Hour
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about When To Use Brackets Or Parentheses In Domain And Range . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.