Which Is Bigger 1 2 Or 2 3
Kalali
Jul 31, 2025 · 5 min read
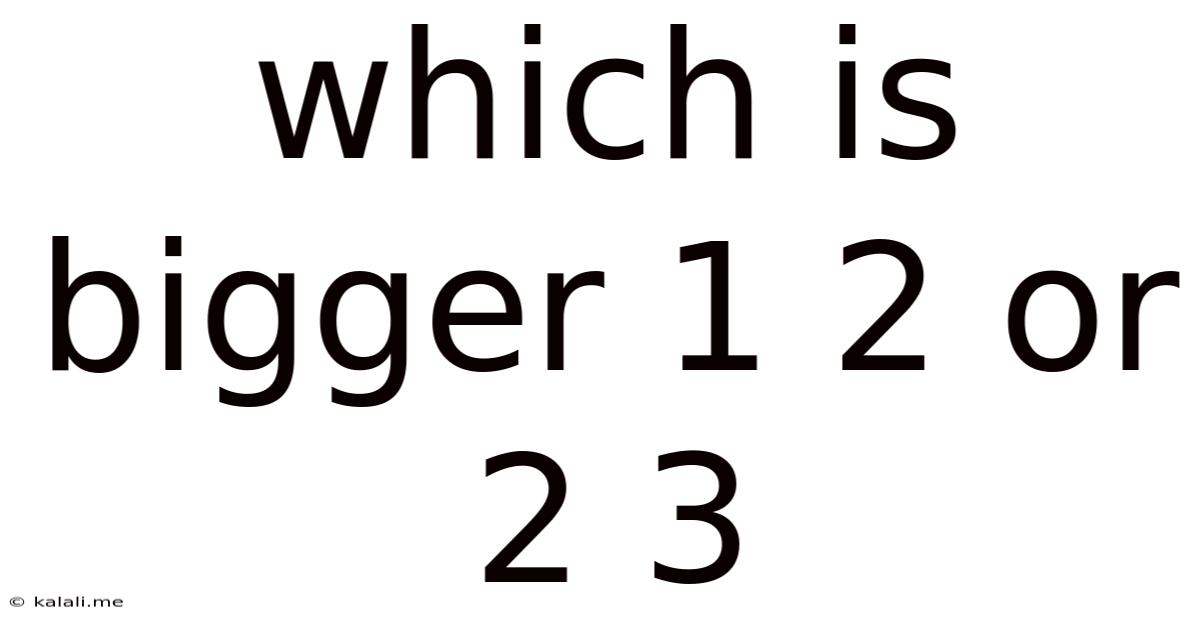
Table of Contents
Which is Bigger: 1/2 or 2/3? A Deep Dive into Fraction Comparison
This seemingly simple question, "Which is bigger: 1/2 or 2/3?", is a great starting point for understanding fundamental concepts in mathematics, particularly fractions. While the answer might seem immediately obvious to some, a deeper exploration reveals valuable insights into fraction comparison techniques, their practical applications, and even the importance of visual representation in mathematical understanding. This article will not only answer the question definitively but also equip you with the skills to compare any two fractions confidently.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's quickly revisit the basics of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) tells us we have one part, and the denominator (2) tells us the whole is divided into two equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and reliable method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of their numerators.
To find a common denominator for 1/2 and 2/3, we need to find the least common multiple (LCM) of 2 and 3. The LCM is the smallest number that is a multiple of both 2 and 3. In this case, the LCM is 6.
Now, we rewrite each fraction with a denominator of 6:
- 1/2: To change the denominator from 2 to 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- 2/3: To change the denominator from 3 to 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
Now the comparison is straightforward: 3/6 versus 4/6. Since 4 > 3, we conclude that 2/3 is bigger than 1/2.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into decimals. This method is particularly useful when dealing with more complex fractions or when a numerical comparison is preferred.
- 1/2: 1 divided by 2 = 0.5
- 2/3: 2 divided by 3 ≈ 0.6667
Comparing the decimal values, 0.6667 > 0.5, confirming that 2/3 is bigger than 1/2. Note that the decimal representation of 2/3 is a repeating decimal (0.666...).
Method 3: Visual Representation
Visual aids can significantly improve understanding, especially for those who find abstract mathematical concepts challenging. Consider representing each fraction using a pie chart or a bar graph.
Imagine two identical circles.
- For 1/2, divide the circle into two equal halves and shade one half.
- For 2/3, divide the circle into three equal thirds and shade two thirds.
Visually comparing the shaded areas clearly shows that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual confirmation reinforces the mathematical conclusion.
Method 4: Cross-Multiplication
This method offers a quick way to compare fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other and vice-versa.
- Multiply the numerator of 1/2 (which is 1) by the denominator of 2/3 (which is 3): 1 x 3 = 3
- Multiply the numerator of 2/3 (which is 2) by the denominator of 1/2 (which is 2): 2 x 2 = 4
Compare the results: 3 < 4. Since the result of the cross-multiplication involving 2/3 is larger, 2/3 is bigger than 1/2.
Practical Applications of Fraction Comparison
Understanding fraction comparison isn't just an academic exercise. It has numerous practical applications in everyday life and various professions:
- Cooking and Baking: Following recipes often requires understanding and adjusting fractional measurements.
- Construction and Engineering: Precise measurements and calculations involving fractions are crucial for accurate construction.
- Finance and Budgeting: Managing finances and understanding proportions requires a strong grasp of fractions.
- Data Analysis: Interpreting data often involves comparing fractions and proportions.
- Science and Research: Many scientific calculations and data interpretations rely heavily on fractional representations.
Beyond the Basics: Comparing More Complex Fractions
The methods discussed above can be applied to compare fractions of any complexity. For example, let's compare 5/8 and 7/12.
Using the Common Denominator Method:
The LCM of 8 and 12 is 24.
- 5/8 = (5 x 3) / (8 x 3) = 15/24
- 7/12 = (7 x 2) / (12 x 2) = 14/24
Since 15 > 14, 5/8 is bigger than 7/12.
Using the Decimal Conversion Method:
- 5/8 = 0.625
- 7/12 ≈ 0.5833
Again, 0.625 > 0.5833, confirming that 5/8 is bigger than 7/12.
Using Cross-Multiplication:
- 5 x 12 = 60
- 7 x 8 = 56
Since 60 > 56, 5/8 is bigger than 7/12.
Conclusion:
The question of which is bigger, 1/2 or 2/3, serves as a springboard for understanding fundamental concepts in fraction comparison. Several methods, each with its own strengths, exist for comparing fractions effectively. Mastering these techniques is crucial not only for academic success but also for navigating various aspects of daily life that involve proportional reasoning and numerical analysis. Remember, visual aids can greatly enhance understanding, and practice is key to building confidence and proficiency in working with fractions. So, next time you encounter a fraction comparison problem, remember the methods outlined here and tackle it with confidence.
Latest Posts
Latest Posts
-
How Many Minutes Are In 360 Seconds
Aug 03, 2025
-
How To Calculate Square Feet Into Linear Feet
Aug 03, 2025
-
What Is A 56 Out Of 60
Aug 03, 2025
-
How Long Does Brandy Melville Take To Ship
Aug 03, 2025
-
Which Element Is More Likely To Become A Anion
Aug 03, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 2 Or 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.