Which Is Bigger 1 2 Or 5 8
Kalali
Jul 18, 2025 · 5 min read
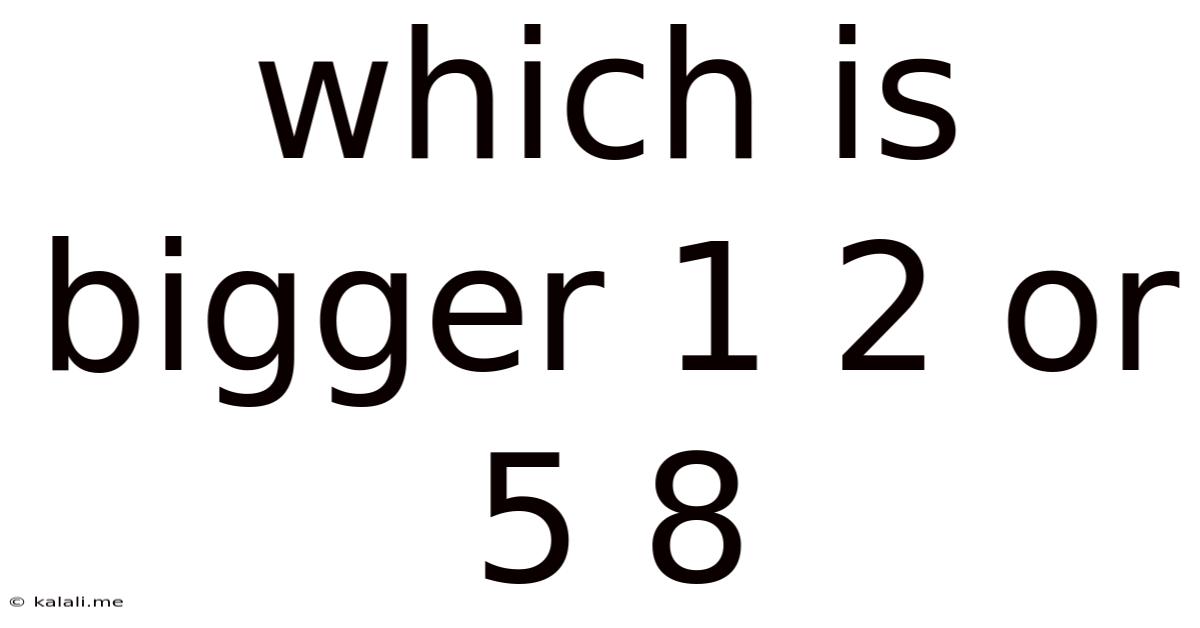
Table of Contents
Which is Bigger: 1/2 or 5/8? A Deep Dive into Fraction Comparison
This seemingly simple question – which is bigger, 1/2 or 5/8? – offers a fantastic opportunity to delve into the world of fractions, exploring various methods for comparison, and highlighting the importance of understanding fundamental mathematical concepts. While the answer might seem obvious to some, understanding why one fraction is larger than another is crucial for developing a strong foundation in mathematics and problem-solving skills. This article will not only answer the question directly but also equip you with the tools to compare any two fractions with confidence.
Meta Description: Learn how to compare fractions effectively! This comprehensive guide explains which is bigger, 1/2 or 5/8, using multiple methods, solidifying your understanding of fraction comparisons and building a strong mathematical foundation.
Understanding Fractions: The Basics
Before we jump into comparing 1/2 and 5/8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator is 1 (we have one part), and the denominator is 2 (the whole is divided into two equal parts).
Method 1: Finding a Common Denominator
This is arguably the most common and reliable method for comparing fractions. The core principle is to rewrite both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
To find a common denominator for 1/2 and 5/8, we need to find a number that is a multiple of both 2 and 8. In this case, 8 is a multiple of 2 (2 x 4 = 8), so 8 is our common denominator.
- Converting 1/2: To convert 1/2 to have a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
Now we can compare:
- 4/8 and 5/8
Since both fractions have the same denominator (8), we simply compare their numerators: 4 and 5. Clearly, 5 is greater than 4. Therefore:
5/8 > 1/2
This method works flawlessly for any pair of fractions, regardless of their complexity. The key is to find the least common multiple (LCM) of the denominators for the most efficient calculation. Finding the LCM can sometimes be tricky with larger numbers; however, using prime factorization can simplify this process.
Method 2: Converting to Decimals
Another effective method involves converting the fractions to their decimal equivalents. This approach is particularly helpful when dealing with fractions that are difficult to compare using a common denominator.
- Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
- Converting 5/8 to a decimal: 5 ÷ 8 = 0.625
Comparing the decimal equivalents, we see that 0.625 is larger than 0.5. Therefore:
0.625 (5/8) > 0.5 (1/2)
This method offers a straightforward visual comparison, especially when working with calculators or computers. However, it's important to remember that decimal representation can sometimes lead to rounding errors, especially with recurring decimals.
Method 3: Visual Representation
Visual aids, such as pie charts or number lines, can provide an intuitive understanding of fraction comparison. Imagine two identical pies.
- 1/2: One pie is cut into two equal pieces, and you have one piece.
- 5/8: The other pie is cut into eight equal pieces, and you have five pieces.
By visually comparing the portions of each pie, it becomes clear that five-eighths is a larger portion than one-half. This method is excellent for building conceptual understanding, especially for younger learners or those who benefit from visual learning.
Method 4: Cross-Multiplication
This method is a shortcut for comparing fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other, and vice versa.
-
Cross-multiply 1/2 and 5/8:
- (1 x 8) = 8
- (5 x 2) = 10
Since 10 > 8, the fraction that resulted in the larger product (5/8) is the larger fraction. Therefore:
5/8 > 1/2
While efficient, this method requires careful attention to avoid errors. Remember to always compare the products correctly.
Practical Applications and Extending the Concept
Understanding fraction comparison isn't just about solving abstract mathematical problems; it has numerous practical applications in everyday life. Consider these examples:
- Cooking: Following recipes often requires understanding fractions for precise measurements of ingredients. Comparing fractions helps determine the appropriate quantities.
- Construction: Accurate measurements are vital in construction, and the ability to compare fractions ensures precision in cutting materials or calculating dimensions.
- Finance: Understanding fractions is essential for managing personal finances, calculating percentages, and interpreting financial data.
Beyond 1/2 and 5/8: The methods described above can be applied to compare any two fractions. For instance, let's compare 7/12 and 2/3:
Using the common denominator method:
- The least common multiple of 12 and 3 is 12.
- 2/3 is equivalent to 8/12 (2 x 4 / 3 x 4).
- Comparing 7/12 and 8/12, we see that 8/12 > 7/12. Therefore, 2/3 > 7/12.
Using cross-multiplication:
- (7 x 3) = 21
- (2 x 12) = 24
- Since 24 > 21, 2/3 > 7/12.
Remember, the choice of method depends on personal preference and the specific fractions being compared. Practicing different methods will build your confidence and understanding of fractions.
Conclusion: Mastering Fraction Comparison
Determining which is bigger, 1/2 or 5/8, might appear trivial at first glance. However, understanding the underlying principles of fraction comparison is fundamental to mathematical literacy. This article explored various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – providing a comprehensive approach to comparing fractions. By mastering these techniques, you'll be well-equipped to handle more complex fraction problems and apply this knowledge to various real-world scenarios. The key to success lies in consistent practice and a solid grasp of the fundamental concepts. So grab a pencil, practice these methods, and watch your fraction-comparison skills soar!
Latest Posts
Latest Posts
-
How Much Is 136 Kg In Pounds
Jul 18, 2025
-
If I M 30 What Year Was I Born
Jul 18, 2025
-
Who Did Bobby Marry From Lizard Lick
Jul 18, 2025
-
Match Each Artist With One Of His Best Known Works
Jul 18, 2025
-
How Many Yards Are In A Block
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 2 Or 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.