Which Is Bigger 1 4 Or 1 8
Kalali
Jul 31, 2025 · 5 min read
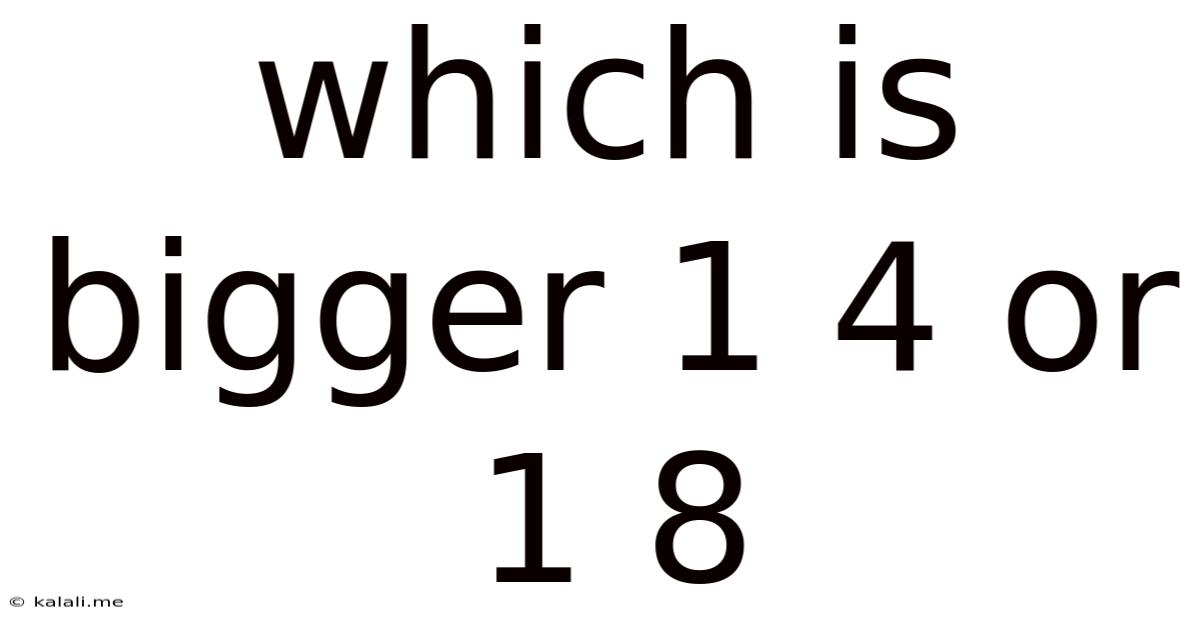
Table of Contents
Decoding Fractions: Which is Bigger, 1/4 or 1/8? A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and a seemingly simple question like "which is bigger, 1/4 or 1/8?" can unlock a deeper appreciation of these numerical representations. This article will not only answer this question definitively but also delve into the underlying concepts, providing a comprehensive guide suitable for various levels of mathematical understanding. We'll explore different methods for comparing fractions, visualize them, and relate them to real-world scenarios.
Meta Description: This in-depth guide explains which fraction, 1/4 or 1/8, is larger, utilizing various comparison methods, visualizations, and real-world examples to solidify understanding of fractional concepts.
Understanding Fractions: A Quick Refresher
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts. The numerator (1) indicates we are considering one of those four parts.
Similarly, 1/8 represents one part out of eight equal parts of a whole.
Comparing 1/4 and 1/8: Visualizing the Fractions
One of the simplest ways to compare fractions is through visualization. Imagine a pizza cut into four equal slices (representing 1/4). Now imagine another pizza, identical in size, cut into eight equal slices (representing 1/8).
If you take one slice from the pizza cut into four slices (1/4), you have a larger piece than if you take one slice from the pizza cut into eight slices (1/8). This visual representation clearly demonstrates that 1/4 is larger than 1/8.
Comparing Fractions with the Same Numerator: A Simple Rule
When comparing two fractions with the same numerator (in this case, both are 1), the fraction with the smaller denominator represents the larger portion. This is because the whole is divided into fewer parts, making each part larger.
Therefore, since the denominator of 1/4 (4) is smaller than the denominator of 1/8 (8), 1/4 is greater than 1/8. This rule provides a quick and efficient method for comparing fractions with identical numerators.
Comparing Fractions Using Decimal Equivalents
Another effective method is converting the fractions into decimal equivalents. To do this, simply divide the numerator by the denominator:
- 1/4 = 1 ÷ 4 = 0.25
- 1/8 = 1 ÷ 8 = 0.125
Comparing the decimal equivalents, 0.25 is clearly greater than 0.125, confirming that 1/4 > 1/8. This method is particularly useful when dealing with more complex fractions or when comparing fractions with different numerators and denominators.
Using a Common Denominator for Comparison
A more general method for comparing any two fractions involves finding a common denominator. This means finding a number that is a multiple of both denominators. In this case, the least common multiple of 4 and 8 is 8.
We then convert both fractions to have a denominator of 8:
- 1/4 = (1 x 2) / (4 x 2) = 2/8
- 1/8 remains 1/8
Now, comparing 2/8 and 1/8, it's evident that 2/8 (which is equivalent to 1/4) is larger than 1/8. This method is versatile and applicable to comparing any pair of fractions, regardless of their numerators and denominators.
Real-World Applications: Understanding the Difference
The difference between 1/4 and 1/8 might seem insignificant in isolation, but in real-world scenarios, it can have significant implications. Consider these examples:
- Baking: A recipe calling for 1/4 cup of sugar versus 1/8 cup of sugar will result in a noticeably different sweetness level.
- Measurements: In construction or engineering, a difference of 1/8 inch compared to 1/4 inch can impact precision and accuracy, potentially affecting the final outcome.
- Data Representation: In data analysis or statistics, the difference between 1/4 and 1/8 of a data set can represent a significant disparity in the analyzed values.
Extending the Concept: Comparing Other Fractions
The principles discussed above can be extended to comparing other fractions. For instance, to compare 3/4 and 5/8, we can use the common denominator method:
- Find the least common multiple of 4 and 8, which is 8.
- Convert 3/4 to have a denominator of 8: (3 x 2) / (4 x 2) = 6/8
- Compare 6/8 and 5/8: 6/8 > 5/8, therefore 3/4 > 5/8.
Beyond Simple Fractions: Exploring More Complex Scenarios
While this article focuses on comparing simple fractions, the principles discussed are applicable to more complex scenarios involving mixed numbers (e.g., 1 1/2), improper fractions (e.g., 5/4), and even fractions with larger numbers. Understanding the fundamental concepts of numerators, denominators, and finding common denominators is crucial for tackling these more challenging comparisons.
Mastering Fractions: A Continuous Learning Process
The ability to compare fractions efficiently is a cornerstone of mathematical understanding. It's not just about rote memorization but about grasping the underlying concepts and applying them to various situations. Practice is key to mastering fraction comparison, and by working through different examples and applying various methods, you'll develop a strong intuition for these numerical representations. Regular practice with exercises and real-world applications will solidify your understanding and allow you to confidently tackle even the most complex fraction problems.
Conclusion: The Significance of Understanding Fractions
The seemingly simple question of which is larger, 1/4 or 1/8, opens the door to a more profound understanding of fractions and their importance in numerous aspects of life. From baking a cake to building a bridge, understanding fractional concepts allows for precision, accuracy, and problem-solving in a wide array of contexts. Mastering fraction comparison is not just a mathematical skill; it's a crucial tool for navigating and understanding the quantitative world around us. Continuous learning and practice will empower you to confidently handle any fractional challenge that comes your way.
Latest Posts
Latest Posts
-
How Many Tablespoons Are In A Packet Of Ranch Seasoning
Aug 03, 2025
-
How Many Minutes Are In 360 Seconds
Aug 03, 2025
-
How To Calculate Square Feet Into Linear Feet
Aug 03, 2025
-
What Is A 56 Out Of 60
Aug 03, 2025
-
How Long Does Brandy Melville Take To Ship
Aug 03, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 4 Or 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.