Which Is Greater 2 3 Or 2 4
Kalali
Jul 01, 2025 · 5 min read
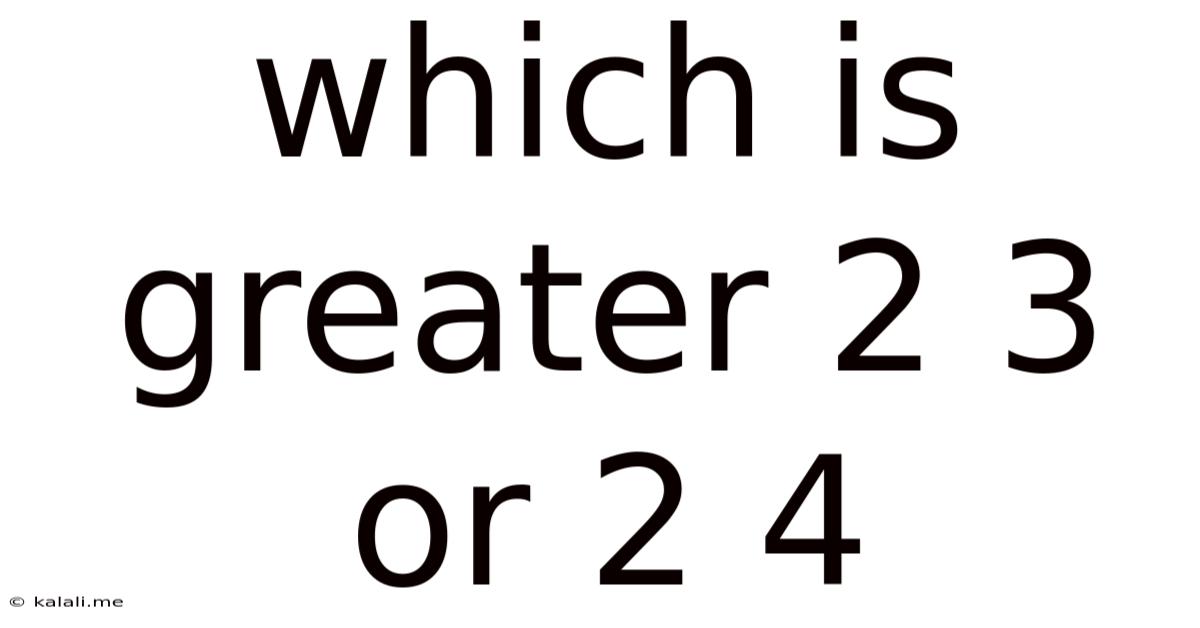
Table of Contents
Which is Greater: 2³ or 2⁴? A Deep Dive into Exponents and Their Applications
This seemingly simple question – which is greater, 2³ or 2⁴ – opens the door to a fascinating exploration of exponents, their properties, and their wide-ranging applications in mathematics, science, and computer science. While the answer itself is straightforward, understanding the underlying concepts is crucial for grasping more complex mathematical ideas. This article will not only answer the question definitively but also delve into the broader context of exponential notation, providing a robust foundation for anyone seeking a deeper understanding.
Meta Description: Uncover the answer to the question, "Is 2³ greater than 2⁴?" This comprehensive guide explores exponents, their properties, and real-world applications, offering a thorough understanding of exponential notation and its significance.
Understanding Exponents
Before we tackle the comparison, let's establish a firm understanding of what exponents represent. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the expressions 2³ and 2⁴, the number 2 is the base, and the numbers 3 and 4 are the exponents.
- 2³ (two cubed or two to the power of three): This means 2 multiplied by itself three times: 2 x 2 x 2 = 8.
- 2⁴ (two to the power of four): This means 2 multiplied by itself four times: 2 x 2 x 2 x 2 = 16.
Directly Answering the Question: 2³ vs. 2⁴
From the calculations above, it's clear that 2⁴ (16) is greater than 2³ (8). This simple comparison highlights a fundamental property of exponents: for a base greater than 1, increasing the exponent leads to a larger result.
Exploring the Properties of Exponents
The comparison between 2³ and 2⁴ is a springboard to understanding several key properties of exponents:
-
Product of Powers: When multiplying two numbers with the same base, you add the exponents. For example, 2³ x 2² = 2⁽³⁺²⁾ = 2⁵ = 32. This property is frequently used in simplifying algebraic expressions and solving equations.
-
Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents. For example, 2⁵ ÷ 2² = 2⁽⁵⁻²⁾ = 2³ = 8. This property is essential for simplifying fractions and working with rational expressions.
-
Power of a Power: When raising a power to another power, you multiply the exponents. For example, (2²)³ = 2⁽²ˣ³⁾ = 2⁶ = 64. This property simplifies complex exponential expressions and is crucial in calculus and advanced algebra.
-
Power of a Product: When raising a product to a power, you raise each factor to that power. For example, (2 x 3)² = 2² x 3² = 4 x 9 = 36. This property is valuable in simplifying expressions involving multiple variables.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power. For example, (2/3)² = 2²/3² = 4/9. This property is essential for simplifying rational expressions and working with fractions raised to powers.
-
Zero Exponent: Any nonzero number raised to the power of zero is equal to 1. For example, 2⁰ = 1. This property seems counterintuitive at first but is a consistent result of the properties discussed above.
-
Negative Exponent: A negative exponent indicates a reciprocal. For example, 2⁻² = 1/2² = 1/4. This property is essential for working with scientific notation and representing very small numbers.
Real-World Applications of Exponents
The concept of exponents isn't confined to theoretical mathematics; it has extensive real-world applications across various fields:
-
Compound Interest: The power of compounding interest is a direct consequence of exponential growth. The formula A = P(1 + r/n)ⁿᵗ, where A is the future value, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years, showcases the exponential growth of investments over time. Understanding exponents is crucial for financial planning and investment strategies.
-
Population Growth: Population growth models often utilize exponential functions to predict future population sizes. Factors like birth rates, death rates, and migration patterns influence the rate of exponential growth. Understanding exponential growth is vital in demography and resource management.
-
Radioactive Decay: Radioactive decay follows an exponential decay model. The formula N(t) = N₀e⁻λt, where N(t) is the amount of the substance remaining after time t, N₀ is the initial amount, λ is the decay constant, and e is the base of the natural logarithm, shows the exponential decrease in radioactive material over time. This is crucial in nuclear physics, medicine (radioactive dating and treatment), and environmental science.
-
Computer Science: Exponents are fundamental in computer science. Binary numbers, the basis of all digital computation, utilize powers of 2. Data structures like trees and graphs often involve exponential relationships. The efficiency of algorithms is frequently analyzed using Big O notation, which often involves exponential functions. Understanding exponents is crucial for optimizing algorithms and developing efficient software.
Beyond 2³ and 2⁴: Exploring Larger Bases and Exponents
While our initial comparison focused on 2³ and 2⁴, the principles extend to larger bases and exponents. Consider the following examples:
-
10³ vs. 10⁴: 10³ = 1000, and 10⁴ = 10000. Again, the higher exponent results in a larger number.
-
3³ vs. 3⁴: 3³ = 27, and 3⁴ = 81. The pattern holds true for other bases.
-
Exploring fractional exponents: Fractional exponents represent roots. For instance, 2^(1/2) is the square root of 2 (approximately 1.414), and 2^(1/3) is the cube root of 2 (approximately 1.260). Understanding fractional exponents expands the scope of exponential notation to include roots and radicals.
Conclusion: The Significance of Understanding Exponents
The seemingly simple question of comparing 2³ and 2⁴ serves as a gateway to a much broader understanding of exponents. Their properties underpin many mathematical concepts, and their applications extend across diverse fields. Mastering exponents is not merely about calculating numerical values; it's about gaining a deeper understanding of exponential growth and decay, which are fundamental processes observed in the natural world and utilized in numerous technological applications. This knowledge provides a strong foundation for tackling more advanced mathematical concepts and real-world problems involving exponential relationships. From financial modeling to understanding the decay of radioactive materials, the power of exponents continues to be a critical tool across numerous disciplines. Therefore, a firm grasp of this fundamental concept is essential for anyone pursuing a path in STEM fields or any area requiring quantitative analysis.
Latest Posts
Latest Posts
-
How Many Minutes Are In 10 Miles
Jul 02, 2025
-
How Many Milliseconds Are In A Day
Jul 02, 2025
-
If Your 16 What Year Were You Born
Jul 02, 2025
-
Ten Thousand 2 Hundrad And 14 How To Writew Numercally
Jul 02, 2025
-
What Is Half Of 1 And 3 4 Cup
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about Which Is Greater 2 3 Or 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.