Which Is Larger 2 3 Or 3 4
Kalali
Jul 29, 2025 · 5 min read
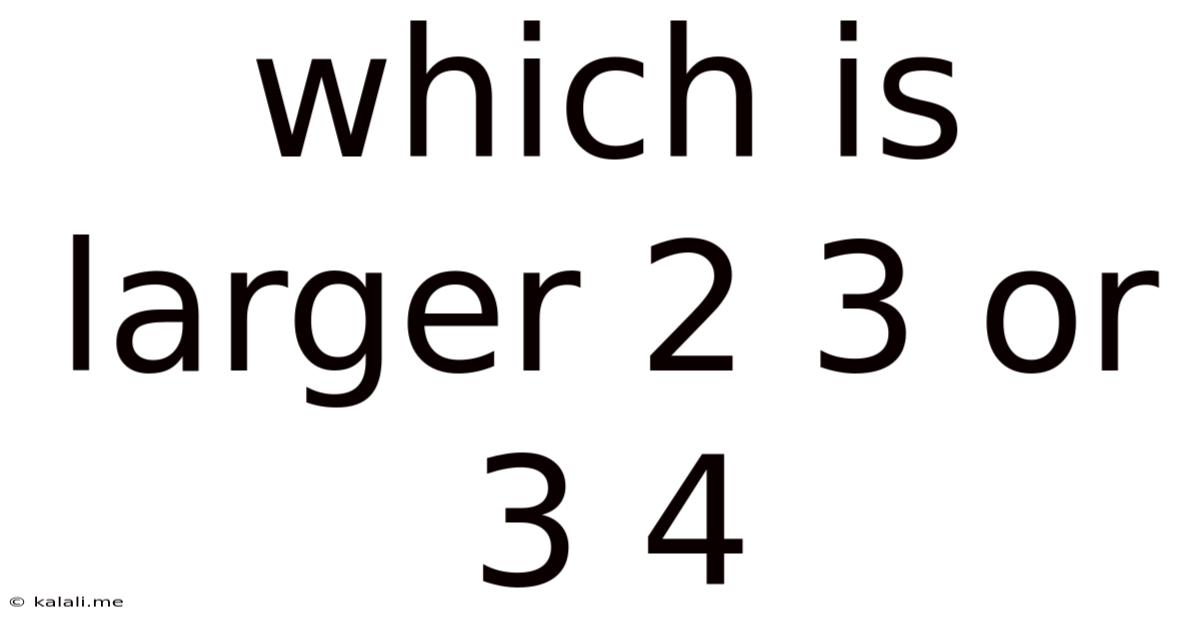
Table of Contents
Which is Larger: 2/3 or 3/4? A Deep Dive into Fraction Comparison
This seemingly simple question – which is larger, 2/3 or 3/4? – offers a fantastic opportunity to explore fundamental mathematical concepts and hone critical thinking skills. While the answer might seem obvious to some, understanding why one fraction is larger than the other is crucial for building a solid mathematical foundation. This article will not only answer the question definitively but also delve into multiple methods for comparing fractions, highlighting their strengths and weaknesses, and ultimately empowering you to confidently tackle similar comparisons in the future.
Meta Description: Learn how to compare fractions effectively! This comprehensive guide explains multiple methods to determine which fraction is larger, using 2/3 and 3/4 as examples. Master fraction comparison and build a stronger mathematical foundation.
Understanding Fractions: A Quick Recap
Before we dive into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 2/3, the denominator (3) tells us the whole is divided into three equal parts, and the numerator (2) tells us we're considering two of those parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The core idea is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 2/3 and 3/4, we need to find the least common multiple (LCM) of 3 and 4. The LCM is the smallest number that is a multiple of both 3 and 4. In this case, the LCM is 12.
Now, we rewrite each fraction with a denominator of 12:
- 2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
- 3/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
Now the comparison is simple: 8/12 versus 9/12. Since 9 > 8, we can conclude that 3/4 is larger than 2/3.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when a decimal representation is needed for other calculations.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
- 2/3: 2 ÷ 3 ≈ 0.6667
- 3/4: 3 ÷ 4 = 0.75
By comparing the decimal values, we see that 0.75 > 0.6667, confirming that 3/4 is larger than 2/3. This method is straightforward but might involve rounding depending on the fraction, potentially introducing a slight margin of error.
Method 3: Visual Representation
While less suitable for complex fractions, visualizing fractions can be a helpful method, especially for beginners. Imagine two identical circles.
- Divide the first circle into three equal parts and shade two of them (representing 2/3).
- Divide the second circle into four equal parts and shade three of them (representing 3/4).
By visually comparing the shaded areas, it becomes apparent that the shaded portion of the second circle (3/4) is larger than the shaded portion of the first circle (2/3). This method provides a clear intuitive understanding of the comparison.
Method 4: Cross-Multiplication
This method offers an efficient way to compare fractions without finding a common denominator. We cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (2) by the denominator of the second fraction (4): 2 x 4 = 8
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (3): 3 x 3 = 9
Compare the results: 8 < 9. Since the product of the second fraction's numerator and the first fraction's denominator is larger, it indicates that 3/4 is larger than 2/3.
Choosing the Right Method: Considerations and Advantages
Each method offers unique advantages depending on the context and the complexity of the fractions involved.
-
Common Denominator: This is generally the most reliable and easily understood method, especially for beginners. It avoids any rounding errors associated with decimal conversions.
-
Decimal Conversion: This method is advantageous when dealing with fractions that are difficult to convert to a common denominator or when decimal representations are already needed in the problem. However, be mindful of rounding errors.
-
Visual Representation: Excellent for building intuition and understanding, especially for simpler fractions. It’s less practical for complex fractions.
-
Cross-Multiplication: Efficient and avoids finding a common denominator, making it a time-saving method for quick comparisons.
Expanding the Understanding: Applications and Further Exploration
The ability to compare fractions isn't just a theoretical exercise. It has wide-ranging applications in various fields:
-
Baking and Cooking: Following recipes accurately often requires understanding and comparing fractions.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering heavily rely on accurate fraction comparisons.
-
Data Analysis: Interpreting data often involves comparing fractional parts of a whole.
-
Finance: Understanding proportions and ratios in financial calculations requires skillful fraction manipulation.
Furthermore, this fundamental skill forms the basis for more advanced mathematical concepts such as:
-
Algebra: Solving equations and inequalities often involves manipulating fractions.
-
Calculus: Understanding limits and derivatives relies on a solid grasp of fractions.
-
Probability and Statistics: Calculating probabilities and analyzing statistical data frequently necessitates working with fractions.
Conclusion: Mastering Fraction Comparison
Determining whether 2/3 or 3/4 is larger is a stepping stone to mastering a fundamental mathematical skill. By understanding the different methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – you gain a versatile toolkit for comparing fractions confidently. Remember to choose the method that best suits the specific context and your comfort level. Mastering fraction comparison will not only improve your mathematical proficiency but also enhance your problem-solving skills across various disciplines. The ability to accurately and efficiently compare fractions is a valuable asset that extends far beyond the classroom.
Latest Posts
Latest Posts
-
Was Elizabeth Taylor In The Little Rascals
Jul 30, 2025
-
How Many Inches In A 6 Foot Table
Jul 30, 2025
-
A Person Who Buys And Sells Land For Profit
Jul 30, 2025
-
How Long Does It Take To Walk 4 Mi
Jul 30, 2025
-
How Old Is Cherry Valance In The Outsiders
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 2 3 Or 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.