Which Linear Equation Shows A Proportional Relationship
Kalali
Apr 03, 2025 · 5 min read
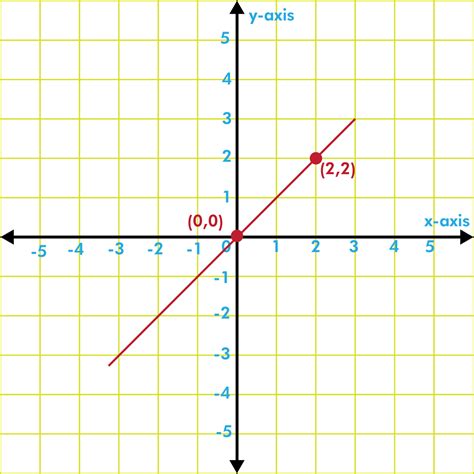
Table of Contents
Which Linear Equation Shows a Proportional Relationship?
Understanding proportional relationships is fundamental in algebra and has far-reaching applications in various fields. This comprehensive guide will delve into the intricacies of linear equations and how to identify those that represent proportional relationships. We'll explore the characteristics of proportional relationships, different forms of linear equations, and provide numerous examples to solidify your understanding. By the end, you'll be able to confidently determine whether a given linear equation signifies a proportional relationship.
What is a Proportional Relationship?
A proportional relationship exists between two variables when their ratio remains constant. This means that as one variable increases or decreases, the other variable changes proportionally. This constant ratio is often referred to as the constant of proportionality or the unit rate. Graphically, a proportional relationship is represented by a straight line passing through the origin (0,0).
Key Characteristics of a Proportional Relationship:
- Constant Ratio: The ratio between the two variables remains constant throughout the relationship.
- Origin Intercept: The line representing the relationship on a graph always passes through the origin (0,0).
- Linear Equation Form: The relationship can be expressed as a linear equation of the form y = kx, where 'k' is the constant of proportionality.
Identifying Proportional Relationships in Linear Equations
Linear equations are fundamental in representing relationships between variables. They are typically expressed in the form y = mx + b, where:
- y and x are the variables.
- m is the slope (representing the rate of change).
- b is the y-intercept (the value of y when x = 0).
A linear equation represents a proportional relationship only when the y-intercept (b) is equal to zero. This is because a proportional relationship requires the line to pass through the origin (0,0), meaning there is no initial value or starting point other than zero.
Different Forms of Linear Equations and Proportional Relationships
Linear equations can be presented in several forms. Let's examine how to identify proportional relationships within each:
1. Slope-Intercept Form (y = mx + b)
In this widely used form, a proportional relationship exists only if b = 0. This simplifies the equation to y = mx, where 'm' is the constant of proportionality (k).
Example 1 (Proportional):
y = 3x
This equation represents a proportional relationship because the y-intercept (b) is 0, and the constant of proportionality (k) is 3. For every increase of 1 in x, y increases by 3.
Example 2 (Not Proportional):
y = 2x + 5
This equation does not represent a proportional relationship because the y-intercept (b) is 5. The line does not pass through the origin.
2. Standard Form (Ax + By = C)
The standard form can be converted to slope-intercept form to determine proportionality. A proportional relationship exists if, after conversion, b = 0. Specifically, if C = 0, the equation represents a proportional relationship.
Example 3 (Proportional):
2x - 5y = 0
Converting to slope-intercept form:
-5y = -2x y = (2/5)x
This equation represents a proportional relationship because b = 0. The constant of proportionality is 2/5.
Example 4 (Not Proportional):
3x + 2y = 6
Converting to slope-intercept form:
2y = -3x + 6 y = (-3/2)x + 3
This equation does not represent a proportional relationship because b = 3.
3. Point-Slope Form (y - y1 = m(x - x1))
While less directly used to identify proportionality, the point-slope form can still be helpful. If the point (x1, y1) is (0,0), and the equation simplifies to y = mx, then it represents a proportional relationship.
Example 5 (Proportional):
y - 0 = 4(x - 0)
This simplifies to y = 4x, indicating a proportional relationship with a constant of proportionality of 4.
Example 6 (Not Proportional):
y - 2 = 1(x - 1)
This simplifies to y = x + 1, which is not a proportional relationship because b = 1.
Real-World Applications of Proportional Relationships
Proportional relationships are prevalent in various real-world scenarios. Understanding them is crucial for solving problems in diverse fields. Here are a few examples:
- Direct Proportion: The cost of purchasing apples is directly proportional to the number of apples bought. If one apple costs $1, then two apples cost $2, and so on.
- Speed and Distance: The distance traveled at a constant speed is directly proportional to the time spent traveling. Double the time, double the distance.
- Unit Conversion: Converting between units like kilograms and pounds or liters and gallons involves proportional relationships.
Solving Problems Involving Proportional Relationships
Let's look at a few problems to solidify our understanding:
Problem 1:
Determine if the equation y = -2x represents a proportional relationship.
Solution:
Yes, this equation represents a proportional relationship because the y-intercept is 0 (b = 0). The constant of proportionality is -2.
Problem 2:
Does the equation 4x + 3y = 12 represent a proportional relationship?
Solution:
No. Let's convert to slope-intercept form:
3y = -4x + 12 y = (-4/3)x + 4
The y-intercept is 4 (b = 4), not 0. Therefore, it does not represent a proportional relationship.
Problem 3:
The number of cookies baked (c) is proportional to the number of batches (b) made. If 2 batches yield 24 cookies, what is the equation that represents this relationship?
Solution:
First, find the constant of proportionality:
k = c/b = 24/2 = 12
The equation representing this proportional relationship is c = 12b.
Advanced Considerations
While this guide focuses on basic linear equations, it's important to note that proportional relationships can extend to more complex mathematical concepts. For instance, in calculus, the concept of proportionality plays a significant role in differential equations and other advanced applications.
Conclusion
Identifying whether a linear equation shows a proportional relationship is a crucial skill in algebra and beyond. By understanding the characteristics of proportional relationships and the different forms of linear equations, you can confidently analyze and solve various mathematical problems arising from real-world applications. Remember that the key indicator is the absence of a y-intercept (b = 0), signifying that the line representing the relationship passes through the origin (0,0). This understanding lays a strong foundation for further exploration of mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
How Is Density Related To The Layers Of The Earth
Apr 03, 2025
-
How Many Pints Are In A Half Gallon
Apr 03, 2025
-
Cuantos Gramos Hay En Una Libra
Apr 03, 2025
-
Is Coca Cola A Homogeneous Mixture
Apr 03, 2025
-
7 To The Power Of 7
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Which Linear Equation Shows A Proportional Relationship . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
