X 1 X 2 X 3
Kalali
May 19, 2025 · 3 min read
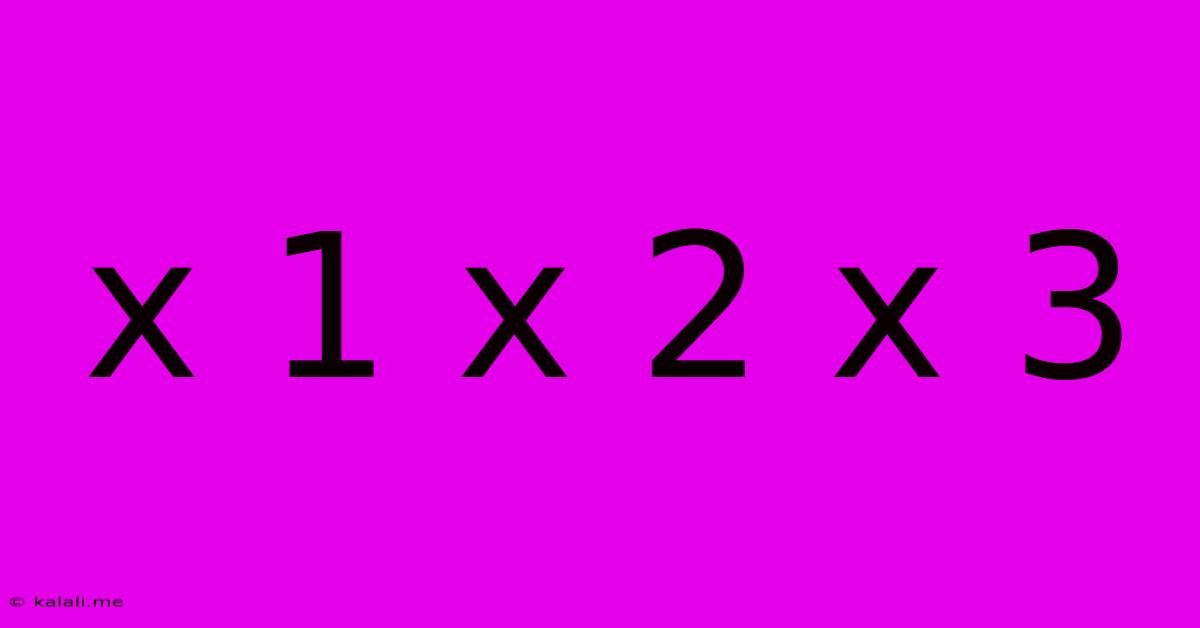
Table of Contents
Decoding the Mystery of x1 x2 x3: Beyond Simple Multiplication
This article explores the multifaceted meaning and application of the expression "x1 x2 x3," moving beyond its straightforward mathematical interpretation to delve into its potential uses in various contexts, including programming, statistics, and even abstract conceptualization. We'll examine how understanding this seemingly simple phrase unlocks a deeper understanding of data manipulation, mathematical modeling, and problem-solving.
What does x1 x2 x3 mean mathematically?
At its most basic level, "x1 x2 x3" represents the multiplication of three variables: x1, x2, and x3. These variables can represent any numerical value, leading to a wide range of possible outcomes. For example, if x1 = 2, x2 = 5, and x3 = 10, then x1 x2 x3 = 100. This simple multiplication forms the foundation for more complex calculations and data analysis.
Beyond Basic Arithmetic: Applications in Different Fields
The seemingly simple "x1 x2 x3" notation has far-reaching applications in numerous fields:
1. Programming and Data Structures
In programming, x1, x2, and x3 often represent elements within an array, a list, or other data structures. The multiplication might represent a calculation performed on these elements, such as calculating the product of three values retrieved from a database or calculating the volume of a rectangular prism given its three dimensions. Consider scenarios involving iterative processes where the values of x1, x2, and x3 change dynamically within a loop.
2. Statistics and Probability
In statistical analysis, these variables might represent independent events or random variables. Their product could be part of a larger formula used in calculating probabilities, correlations, or variances. For instance, calculating the combined probability of three independent events occurring.
3. Physics and Engineering
In physics and engineering, this notation might represent the components of a vector in three-dimensional space or the parameters of a physical system, such as the dimensions of a box (length, width, height), where the product could represent volume or another derived quantity. The concept extends to more complex multi-dimensional systems.
4. Abstract Representation
Beyond its concrete applications, "x1 x2 x3" can serve as an abstract representation of a process or interaction involving three factors or inputs. Think of it as a generalized model where the specific meaning of x1, x2, and x3 is defined within the context of the problem being addressed.
Expanding the Concept: Matrices and Beyond
The concept extends to more complex scenarios. Imagine a scenario where you're dealing with matrices or tensors. The "x1 x2 x3" notation might represent elements within these higher-dimensional data structures, opening possibilities for advanced mathematical operations and model building. These scenarios often arise in machine learning, deep learning, and various scientific computing applications.
Conclusion: The Power of Simplicity
While seemingly simple, the expression "x1 x2 x3" provides a foundation for a broad spectrum of calculations and concepts across diverse fields. Understanding its adaptability and versatility unlocks the potential for more complex mathematical modeling and problem-solving. By appreciating the fundamental building blocks of mathematics, we can build robust and elegant solutions to multifaceted challenges. The true power lies in understanding how this simple expression can be applied within specific contexts to produce meaningful and impactful results.
Latest Posts
Latest Posts
-
Does A Car Battery Charge When Idling
May 19, 2025
-
What Temperature Does A Kettle Boil At
May 19, 2025
-
How To Remove A Snapped Screw
May 19, 2025
-
What Is The Difference Between A Casserole And A Stew
May 19, 2025
-
Smoke Alarm Still Chirps After Replacing Battery
May 19, 2025
Related Post
Thank you for visiting our website which covers about X 1 X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.