X 2 Y 2 1 3 X 2y 3
Kalali
May 24, 2025 · 2 min read
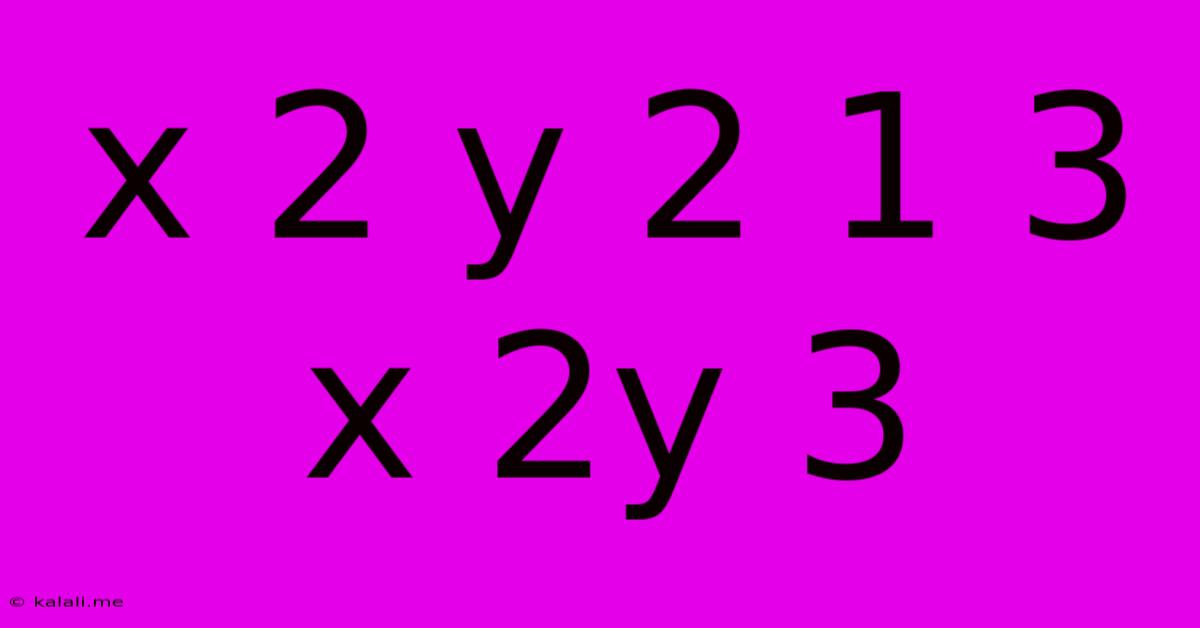
Table of Contents
Solving the Equation x² + 2y² + 1 = 3x + 2y + 3
This article explores how to solve the equation x² + 2y² + 1 = 3x + 2y + 3. We'll break down the process step-by-step, covering techniques for manipulating the equation and finding potential solutions. This problem combines elements of algebra and equation solving, making it a great exercise for practicing these fundamental mathematical skills.
The equation x² + 2y² + 1 = 3x + 2y + 3 appears deceptively simple, but requires a methodical approach to solve. Our goal is to find the values of x and y that satisfy this equation. This involves rearranging the equation into a more manageable form.
Rearranging the Equation
First, let's rearrange the equation to group similar terms together:
x² - 3x + 2y² - 2y + 1 - 3 = 0
Simplifying, we get:
x² - 3x + 2y² - 2y - 2 = 0
Now, we can employ the technique of completing the square for both the x and y terms. Completing the square allows us to transform a quadratic expression into a perfect square trinomial, making it easier to solve.
Completing the Square
Let's complete the square for the x terms:
x² - 3x can be rewritten as (x - 3/2)² - (3/2)² = (x - 3/2)² - 9/4
Similarly, for the y terms:
2y² - 2y can be rewritten as 2(y² - y). To complete the square, we take half of the coefficient of y (-1), square it (1/4), and add and subtract it inside the parentheses:
2(y² - y + 1/4 - 1/4) = 2((y - 1/2)² - 1/4) = 2(y - 1/2)² - 1/2
Substituting these back into our equation:
(x - 3/2)² - 9/4 + 2(y - 1/2)² - 1/2 - 2 = 0
Simplifying and Solving
Now, let's simplify and solve for x and y:
(x - 3/2)² + 2(y - 1/2)² = 9/4 + 1/2 + 2 = 9/4 + 5/4 = 14/4 = 7/2
This equation represents an ellipse. The center of the ellipse is at (3/2, 1/2). There are infinitely many pairs of (x, y) that satisfy this equation. To find specific solutions, you could choose a value for x and solve for y, or vice-versa. Numerical methods or graphing software could be utilized to find approximate solutions.
Conclusion
Solving x² + 2y² + 1 = 3x + 2y + 3 involves several steps, including rearranging the equation, completing the square, and simplifying to reveal the elliptical nature of the solution set. While we cannot find single unique solutions, we have successfully transformed the initial equation into a standard form that allows for graphical representation and the identification of an infinite number of solutions. Understanding these steps is crucial for mastering algebraic manipulation and solving similar quadratic equations.
Latest Posts
Latest Posts
-
Hot Water Heater Settings Top And Bottom
May 25, 2025
-
How To Prove A Function Is Surjective
May 25, 2025
-
What Did Varys Do To The Sorcerer
May 25, 2025
-
How To Remove Paint From A Tub
May 25, 2025
-
Where Is Exp Share In Emerald
May 25, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 1 3 X 2y 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.