X 3 2x 2 X 4
Kalali
Jun 05, 2025 · 2 min read
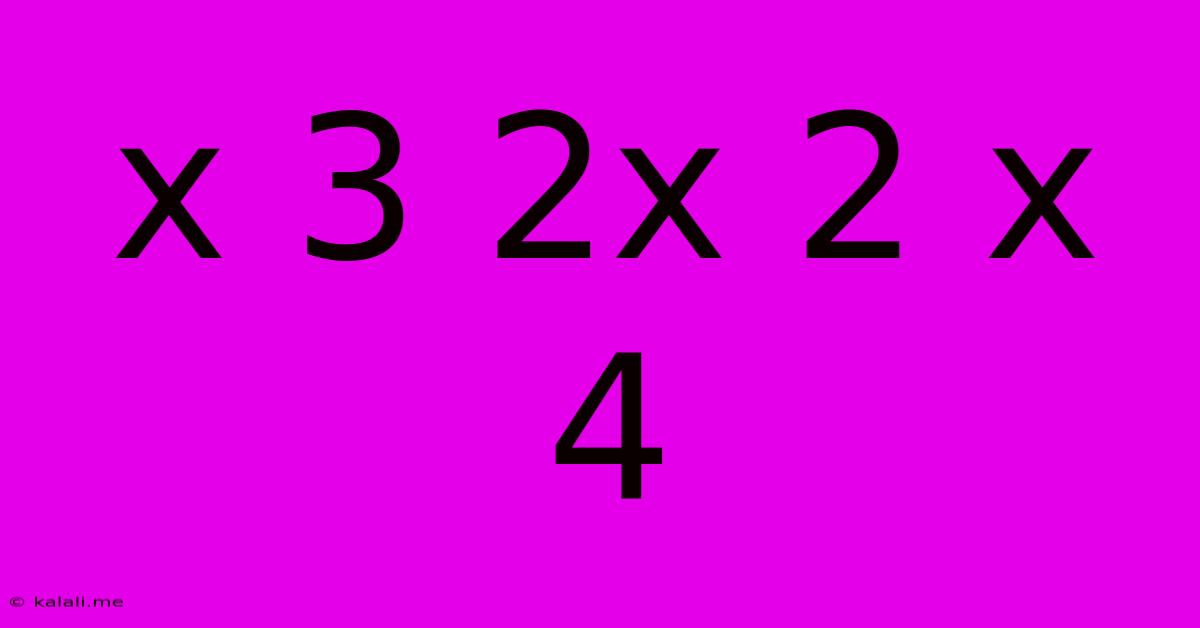
Table of Contents
Decoding the Mathematical Expression: x³ + 2x² + x⁴
This article explores the mathematical expression x³ + 2x² + x⁴, explaining its components, simplification, and potential applications. Understanding this seemingly simple expression opens doors to various mathematical concepts and problem-solving techniques. We'll delve into its structure, explore methods of simplification, and briefly touch on where such expressions might appear in real-world applications.
Understanding the Components
The expression x³ + 2x² + x⁴ is a polynomial. A polynomial is an expression consisting of variables (in this case, 'x') and coefficients, combined using addition, subtraction, and multiplication, but with no division by a variable. Let's break down each term:
-
x³: This term represents 'x' multiplied by itself three times (x * x * x). The '3' is the exponent, indicating the power to which 'x' is raised. This is also known as a cubic term.
-
2x²: This term is composed of a coefficient ('2') and a variable term ('x²'). 'x²' represents 'x' multiplied by itself (x * x), also known as a quadratic term.
-
x⁴: This term represents 'x' multiplied by itself four times (x * x * x * x). The '4' is the exponent, making this a quartic term.
Simplifying the Polynomial
While the expression is already relatively simple, we can improve it by arranging the terms in descending order of their exponents, which is standard polynomial notation. This gives us:
x⁴ + x³ + 2x²
This rearrangement doesn't change the value of the expression, it merely presents it in a more conventional and easily readable format. This standard form makes it easier to perform operations like adding or subtracting other polynomials.
Applications and Further Exploration
Expressions like x⁴ + x³ + 2x² appear frequently in various areas of mathematics and its applications, including:
-
Calculus: This type of polynomial is frequently used in differentiation and integration problems. Finding the derivative or integral of this polynomial would be a standard calculus exercise.
-
Algebra: Solving equations involving this polynomial, perhaps setting it equal to zero to find its roots, is a common algebra problem. Finding the roots involves techniques like factoring or using numerical methods.
-
Physics and Engineering: Polynomials often model physical phenomena. This particular polynomial could represent a curve, a trajectory, or another aspect of a system being modeled mathematically.
Conclusion
The seemingly basic expression x³ + 2x² + x⁴ provides a gateway to understanding fundamental concepts in algebra and calculus. By understanding its components and simplifying it, we lay the foundation for tackling more complex polynomial expressions and their applications in various fields. Further exploration into polynomial manipulation, root finding, and the application of these concepts in problem-solving will enhance mathematical proficiency.
Latest Posts
Latest Posts
-
Why Is Adam So Scarred Dark
Jun 07, 2025
-
Youngs Modlulus Vs Cold Work For A Ductile Material
Jun 07, 2025
-
Single Pole Vs Double Pole Breaker
Jun 07, 2025
-
An Employee Who Appropairty Protized Tasks
Jun 07, 2025
-
How To Dispose Of Lipo Batteries
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.