X 3 3x 2 3x 2
Kalali
Jun 11, 2025 · 2 min read
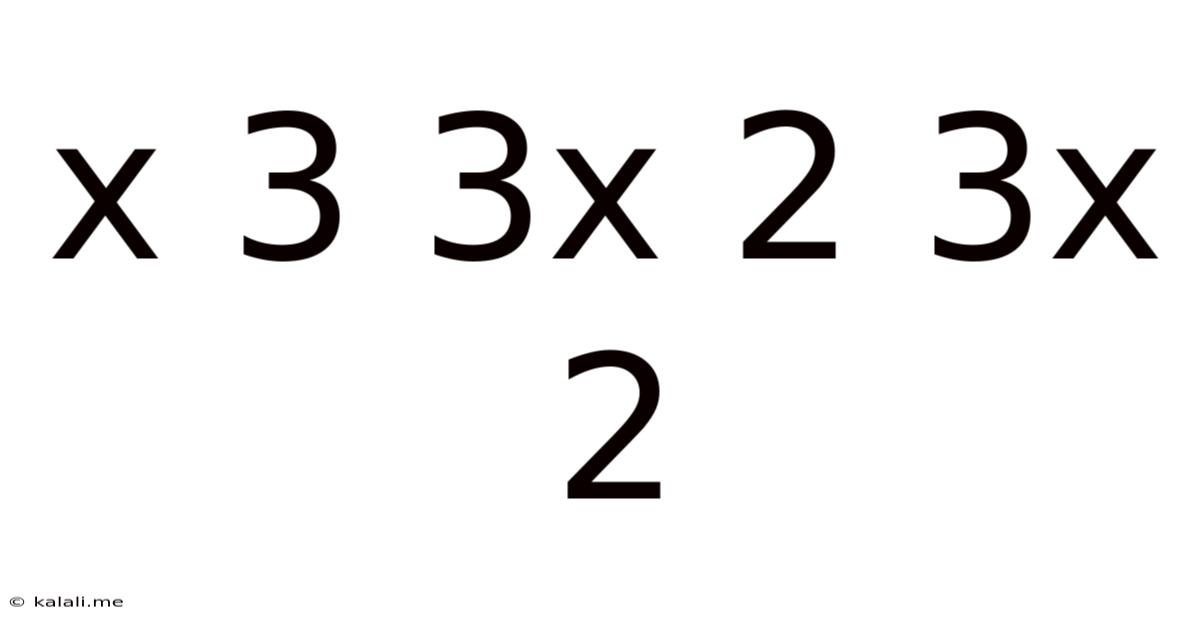
Table of Contents
Deciphering the Mathematical Expression: x³ + 3x² + 3x + 1
This article will explore the mathematical expression x³ + 3x² + 3x + 1, examining its structure, simplification, and potential applications. Understanding this expression involves recognizing its pattern and relating it to fundamental algebraic concepts. We'll uncover its hidden meaning and show you how to approach similar problems.
What is x³ + 3x² + 3x + 1?
At first glance, x³ + 3x² + 3x + 1 might seem like a complex polynomial expression. However, it's a perfect example of a binomial expansion raised to the power of three. This specific polynomial is the expansion of (x + 1)³. This means it's the result of multiplying (x + 1) by itself three times: (x + 1)(x + 1)(x + 1).
Understanding Binomial Expansion
Binomial expansion is a fundamental concept in algebra. It provides a method for expanding expressions of the form (a + b)ⁿ, where 'n' is a positive integer. The binomial theorem gives a formula for determining the coefficients and powers of 'a' and 'b' in the expansion. For (x + 1)³, the binomial theorem leads to the expression:
x³ + 3x² + 3x + 1
Expanding (x+1)³ Manually
Let's demonstrate the expansion manually to further illustrate the point:
- First step: (x + 1)(x + 1) = x² + 2x + 1 (using the FOIL method or distributive property)
- Second step: (x² + 2x + 1)(x + 1) = x³ + x² + 2x² + 2x + x + 1
- Third step (simplification): x³ + 3x² + 3x + 1
This confirms that our original expression, x³ + 3x² + 3x + 1, is indeed the expanded form of (x + 1)³.
Applications and Significance
This seemingly simple polynomial has applications in various fields:
- Calculus: Understanding binomial expansions is crucial for differentiation and integration, particularly in finding derivatives and integrals of complex functions.
- Probability and Statistics: Binomial expansions are fundamental in probability calculations, specifically in binomial probability distributions.
- Physics and Engineering: Many physical phenomena can be modeled using polynomial equations, and understanding their expansion is essential for analysis and prediction.
- Computer Science: Binomial expansions find their use in algorithms and data structures.
Solving Equations Involving x³ + 3x² + 3x + 1
Solving equations where this polynomial is involved often simplifies significantly after recognizing its factored form. For example, if you encounter an equation like:
x³ + 3x² + 3x + 1 = 0
It can be rewritten as:
(x + 1)³ = 0
This directly implies that x = -1 is the only real solution.
Conclusion
The expression x³ + 3x² + 3x + 1, while appearing complex at first, is a straightforward representation of the binomial expansion (x + 1)³. Understanding this connection simplifies its manipulation and reveals its importance in various mathematical and scientific applications. By recognizing patterns and utilizing fundamental algebraic concepts, you can master the simplification and application of such expressions.
Latest Posts
Latest Posts
-
How Many Units Are In 1 Ml
Jul 01, 2025
-
Write An Equation For These Two Complementary Angles
Jul 01, 2025
-
How Do You Beat Bloxorz Level 7
Jul 01, 2025
-
How Old Are You If Your Born In 1992
Jul 01, 2025
-
How Many Quarts Are In 15 Gallons
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.