X 3 Y 3 Z 3
Kalali
May 25, 2025 · 3 min read
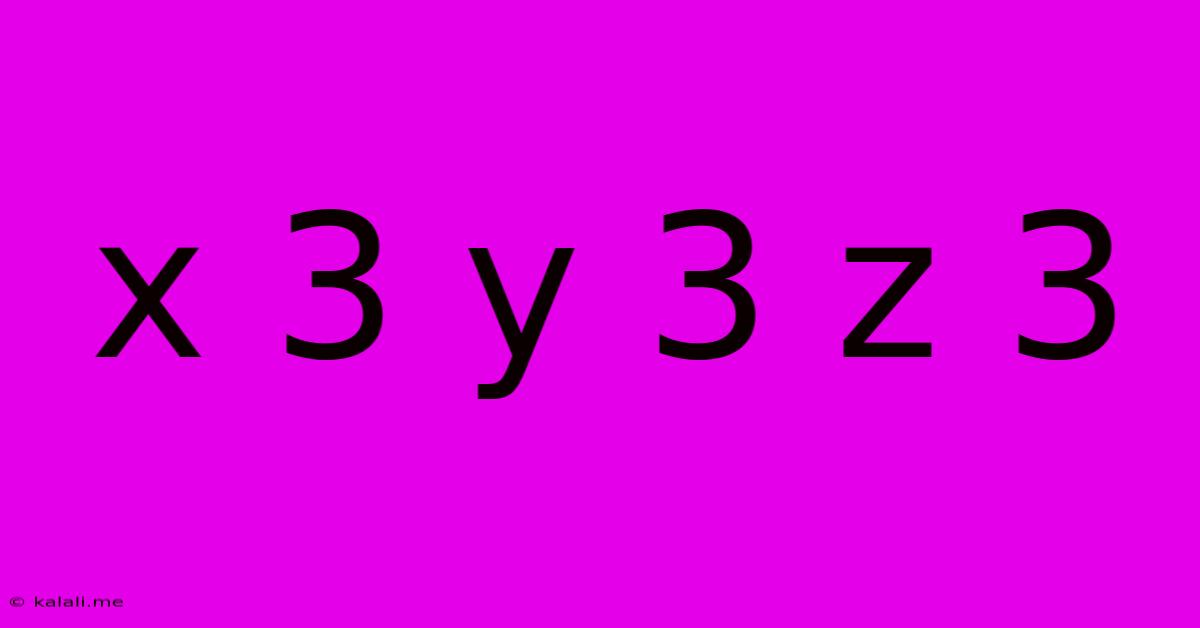
Table of Contents
Unraveling the Mystery of x³ + y³ + z³ = k
The deceptively simple equation x³ + y³ + z³ = k has captivated mathematicians and computer scientists for decades. While seemingly straightforward, finding integer solutions for various values of k presents a surprisingly complex challenge. This article delves into the fascinating world of this cubic equation, exploring its history, significance, and the ongoing quest for solutions.
What Makes x³ + y³ + z³ = k So Challenging?
The equation's difficulty stems from the non-linearity of the cubic terms. Unlike linear equations, which have straightforward solution methods, cubic equations offer a much richer, and often more intractable, landscape of possibilities. Finding integer solutions, in particular, requires sophisticated techniques and significant computational power. For some values of k, solutions are readily apparent; for others, the search can be extensive, even fruitless.
A Brief History of the Problem
The problem of finding integer solutions to x³ + y³ + z³ = k has a rich history, with its roots stretching back to the early days of number theory. While specific instances of the equation have been studied for centuries, the general problem gained significant traction with the advent of powerful computers, allowing for extensive computational searches. The quest to find solutions, especially for larger values of k, has become a benchmark for computational power and algorithmic efficiency.
The Significance of Specific Values of k
The value of k significantly impacts the difficulty of finding solutions. For example:
- k = 0: This case has trivial solutions, such as x = y = z = 0. Beyond these, it boasts infinitely many non-trivial integer solutions.
- k = 1: Solutions are relatively easy to find. One obvious example is x = 1, y = 0, z = 0.
- k = 2: Finding integer solutions to x³ + y³ + z³ = 2 remains incredibly challenging. This specific case has fueled significant research and algorithmic development. It was only recently that a solution was found, highlighting the computational intensity involved.
- k = 3: Like k = 2, finding solutions for this case has proven to be highly challenging. The hunt for solutions continues to push the boundaries of computational mathematics.
- k = 42: The case of k = 42, for years presented a significant challenge for mathematicians. This was solved more recently.
Modern Approaches and Computational Techniques
The search for solutions to x³ + y³ + z³ = k often employs advanced computational techniques, including:
- Sieving methods: These methods efficiently eliminate a vast number of potential solutions based on certain criteria.
- Integer programming: Formulating the problem as an integer programming problem allows for the use of specialized optimization algorithms.
- Distributed computing: The immense computational demands frequently necessitate the use of distributed computing networks to harness the power of multiple machines concurrently.
Ongoing Research and Open Problems
Despite significant advancements, many questions surrounding x³ + y³ + z³ = k remain unanswered. Researchers continue to explore:
- The distribution of solutions: Understanding the patterns and frequency of solutions for different values of k is an ongoing area of research.
- Improved algorithms: The development of more efficient and sophisticated algorithms is crucial for tackling larger and more challenging instances of the equation.
- The existence of solutions: For some values of k, it remains unknown whether integer solutions even exist.
Conclusion
The seemingly simple equation x³ + y³ + z³ = k presents a surprisingly deep and complex mathematical problem. Its continued study pushes the boundaries of computational mathematics and highlights the intricate relationships between seemingly basic mathematical concepts. The quest for solutions remains an active area of research, promising further breakthroughs and a deeper understanding of number theory.
Latest Posts
Latest Posts
-
Bash If File Does Not Exist
May 25, 2025
-
Why Does My Car Ac Smell
May 25, 2025
-
How To Say And In German
May 25, 2025
-
Prime Rib Vs Standing Rib Roast
May 25, 2025
-
Skyrim What Counts As A Skill Enchantment
May 25, 2025
Related Post
Thank you for visiting our website which covers about X 3 Y 3 Z 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.