X 4 X 5 Expand And Simplify
Kalali
Jun 11, 2025 · 2 min read
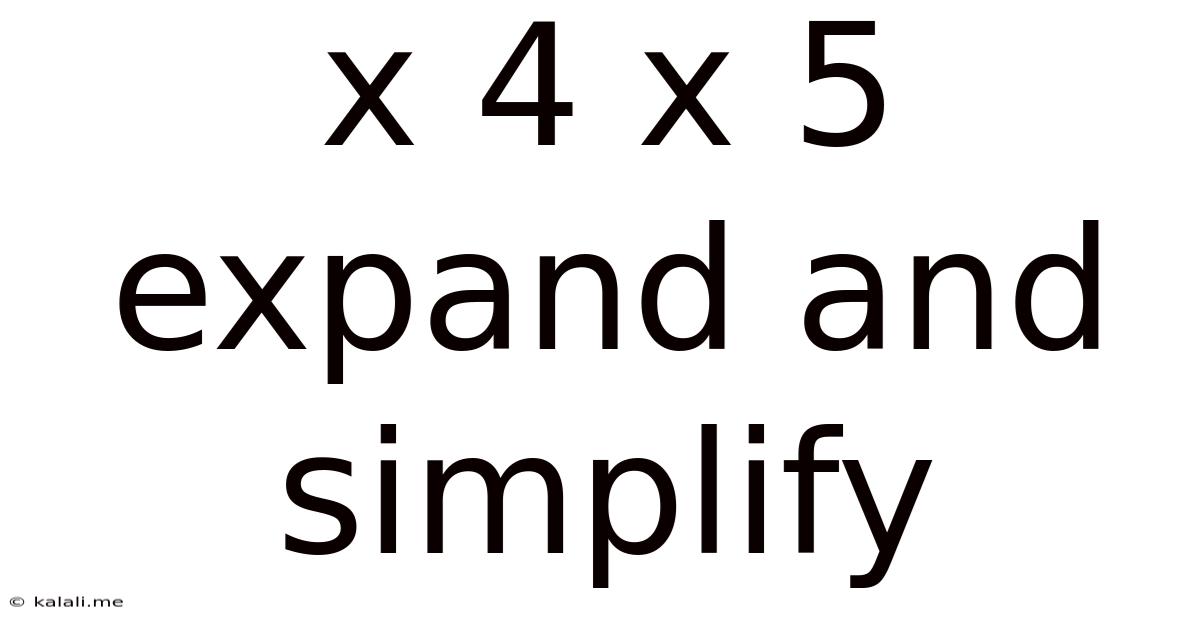
Table of Contents
Expanding and Simplifying x(4)(5): A Step-by-Step Guide
This article will guide you through the process of expanding and simplifying the algebraic expression x(4)(5). Understanding this seemingly simple problem lays the foundation for more complex algebraic manipulations. We'll cover the order of operations, the commutative property, and how to arrive at the most simplified form. This is a fundamental concept in algebra, crucial for students and anyone working with mathematical expressions.
Understanding the Problem:
The expression x(4)(5) involves multiplication of a variable (x) and two constants (4 and 5). Our goal is to simplify this expression into its most concise form, eliminating unnecessary parentheses and combining like terms. This is often encountered in early algebra, and mastering it helps build confidence and proficiency in more advanced topics.
Step 1: Applying the Associative Property of Multiplication
The associative property of multiplication states that the grouping of factors does not change the product. This means we can rearrange the parentheses in our expression without altering its value. We can group the constants together:
x(4)(5) = x(4 x 5)
Step 2: Performing the Multiplication of Constants
Now, we simply multiply the constants 4 and 5:
x(4 x 5) = x(20)
Step 3: Simplifying the Expression
Finally, we can write the expression in its most simplified form by removing the unnecessary parentheses:
x(20) = 20x
Therefore, the expanded and simplified form of x(4)(5) is 20x.
Key Concepts Used:
- Order of Operations (PEMDAS/BODMAS): While not strictly necessary in this specific example due to only multiplication being involved, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is crucial for more complex expressions.
- Associative Property of Multiplication: The order in which we multiply numbers does not affect the result. This allows us to group the constants together for easier calculation.
- Commutative Property of Multiplication: Although not explicitly used here, it's important to note that the commutative property (a x b = b x a) also applies to multiplication. We could have rearranged the expression as (5)(4)(x) and still arrive at the same simplified form.
Practical Applications:
Understanding how to expand and simplify algebraic expressions like x(4)(5) is fundamental to various mathematical applications, including:
- Solving Equations: Simplifying expressions helps in solving equations more efficiently.
- Geometry: Calculating areas and volumes often involves multiplying variables and constants.
- Physics and Engineering: Many formulas in physics and engineering involve manipulating algebraic expressions.
This seemingly straightforward problem provides a solid base for understanding more complex algebraic concepts. By mastering the principles involved, you build a strong foundation for future mathematical challenges. Remember the key steps: apply the associative property, perform the multiplication of constants, and simplify the resulting expression.
Latest Posts
Latest Posts
-
How Many Feet Is Half An Acre
Jul 01, 2025
-
If I Was Born In 2004 How Old Am I
Jul 01, 2025
-
How Long Would It Take To Drive 2000 Miles
Jul 01, 2025
-
What Color Does Black And Blue Make
Jul 01, 2025
-
How To Pass Level 7 In Bloxorz
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 5 Expand And Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.