X Divided By Square Root Of X
Kalali
Jul 02, 2025 · 6 min read
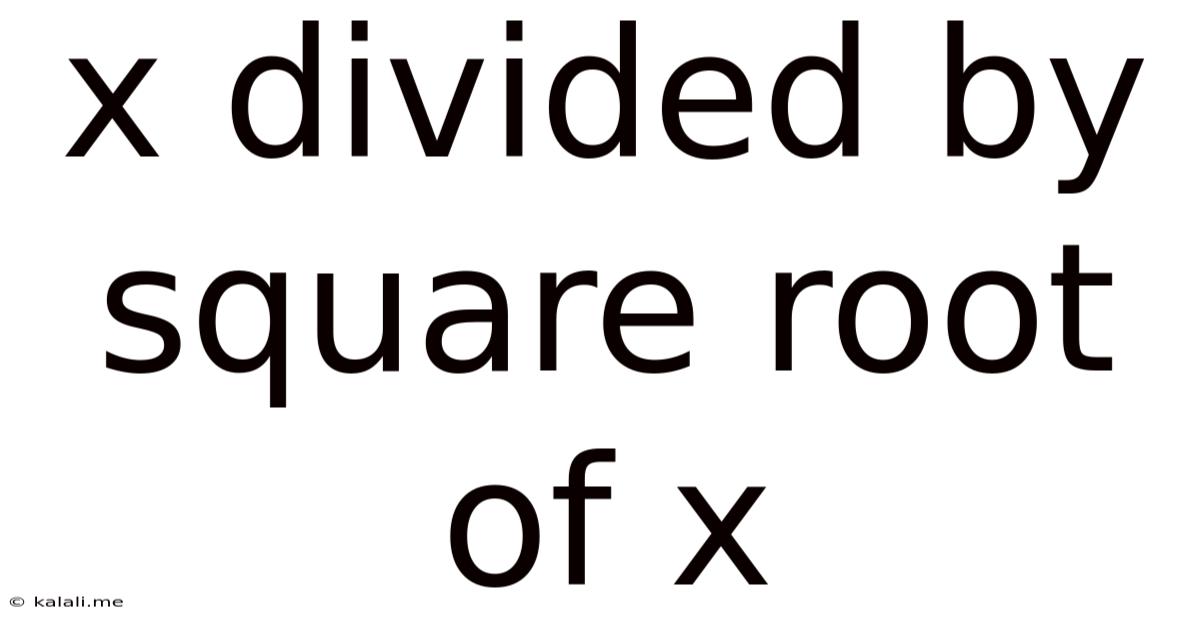
Table of Contents
Exploring the Mathematical Landscape of x Divided by the Square Root of x
This article delves into the fascinating mathematical expression: x divided by the square root of x, exploring its simplification, applications, and implications within various mathematical contexts. We'll unpack the underlying principles, discuss its behavior across different domains, and examine its relevance in real-world scenarios. Understanding this seemingly simple expression unlocks a deeper appreciation for fundamental mathematical operations and their broader applications.
Meta Description: This comprehensive guide explores the mathematical expression x divided by √x, simplifying it, examining its behavior across different domains, and exploring its relevance in various fields. Learn about its applications and implications in a detailed and accessible manner.
Understanding the Basics: Simplifying x / √x
At its core, the expression x / √x represents a division problem. We are dividing a variable x by its square root, √x. The key to simplifying this expression lies in understanding the properties of exponents and radicals. Recall that the square root of a number is equivalent to raising that number to the power of 1/2. Therefore, √x can be rewritten as x<sup>1/2</sup>.
Now, our expression becomes: x / x<sup>1/2</sup>. Using the rules of exponents, specifically the rule for dividing exponential terms with the same base, we subtract the exponents:
x<sup>(1 - 1/2)</sup> = x<sup>1/2</sup>
Therefore, the simplified form of x / √x is √x or x<sup>1/2</sup>, provided that x is a non-negative number. The restriction to non-negative numbers arises because the square root of a negative number is not a real number. We'll delve deeper into the implications of this restriction in the sections below.
Exploring the Domain and Range
The domain of a function represents all possible input values (in this case, x) for which the function is defined. In the case of x / √x, the function is undefined when the denominator, √x, is equal to zero. This occurs when x = 0. Furthermore, the square root of a negative number is not a real number, so x must be non-negative.
Therefore, the domain of the function f(x) = x / √x is (0, ∞), meaning all positive real numbers. The function is not defined at x = 0.
The range of a function represents all possible output values. Since the simplified form of the expression is √x, and the square root of any positive number is always positive, the range of the function is (0, ∞). The function will always produce positive real numbers.
Graphical Representation and Analysis
Visualizing the function f(x) = x / √x = √x through a graph provides further insight into its behavior. The graph will be a curve starting at the origin (0,0), but it doesn't include the point (0,0) itself because the function is undefined at x=0. The curve increases steadily as x increases. This illustrates the positive relationship between x and √x: as x grows larger, so does its square root.
Applications in Calculus and Other Fields
The expression x / √x and its simplified form, √x, appear in various mathematical contexts, particularly within calculus and related fields:
-
Derivatives and Integrals: The derivative of √x is a fundamental result in calculus, often encountered when analyzing the rates of change of functions. Similarly, the integral of √x is also a frequently used result. Understanding the simplification of x / √x is crucial for efficiently working with these calculus operations.
-
Physics and Engineering: Square root functions frequently appear in physics and engineering, often related to concepts like distance, velocity, and acceleration. Understanding the simplification allows for efficient problem-solving and simplification of complex equations. For example, in calculating the velocity of an object under the influence of gravity, square root terms appear frequently.
-
Probability and Statistics: Square roots appear in the formulas for calculating standard deviation and variance, which are fundamental statistical measures. A grasp of the simplification can streamline calculations in these areas.
-
Financial Modeling: Mathematical models used in financial analysis often incorporate square root functions, particularly when dealing with volatility and risk assessment. Again, simplifying the expression can help in efficient modeling.
Exploring Related Concepts: Rationalizing the Denominator
While we've simplified x / √x directly, it's worth exploring a related concept: rationalizing the denominator. This technique is used to eliminate radicals from the denominator of a fraction. While not strictly necessary in this case, it's a valuable algebraic skill.
To rationalize the denominator of x / √x, we can multiply both the numerator and denominator by √x:
(x / √x) * (√x / √x) = (x√x) / x = √x
This leads us back to the same simplified expression we obtained earlier.
Handling Complex Numbers: Extending the Domain
Our previous discussion focused on the real number domain. However, if we extend our consideration to complex numbers, the expression x / √x becomes more nuanced. The square root of a complex number is multi-valued, meaning it can have multiple solutions. This leads to a more complex analysis of the domain and range of the function, requiring the use of complex analysis techniques. For instance, the principal square root is often chosen to maintain consistency.
Numerical Examples and Practical Applications
Let's consider some numerical examples to further illustrate the concept:
-
If x = 4, then x / √x = 4 / √4 = 4 / 2 = 2. This is equal to √4 = 2, demonstrating the simplification.
-
If x = 9, then x / √x = 9 / √9 = 9 / 3 = 3. This is equal to √9 = 3, further confirming the simplification.
-
If x = 0.25, then x / √x = 0.25 / √0.25 = 0.25 / 0.5 = 0.5. This is equal to √0.25 = 0.5.
These examples highlight the consistent simplification across different positive values of x.
Consider a real-world example in physics: Suppose we're calculating the velocity of an object falling under gravity. The distance fallen (d) is proportional to the square root of the time (t) elapsed. Then, velocity, which is the change in distance over the change in time, might involve an expression similar to x / √x, offering a simplified view of the relationship.
Conclusion: A Foundation for Further Exploration
The seemingly simple expression x / √x offers a rich learning opportunity, underscoring the importance of fundamental algebraic manipulation and its implications across various mathematical disciplines. Its simplification to √x highlights the power of exponent rules and provides a foundational understanding that extends into more complex mathematical concepts. Understanding its domain and range, graphical representation, and applications in calculus and other fields demonstrates the practical relevance of this seemingly basic expression. This exploration serves as a stepping stone to a deeper understanding of more advanced mathematical concepts and their application to real-world problems. By understanding this simple yet fundamental operation, we build a solid foundation for further mathematical exploration.
Latest Posts
Latest Posts
-
How Much Does A 35 Pack Of Water Weigh
Jul 03, 2025
-
Is Catherine O Hara Related To Maureen O Hara
Jul 03, 2025
-
What Does Pc Stand For In Business
Jul 03, 2025
-
Opening In A Wall To Let In Air Or Light
Jul 03, 2025
-
How Many Stalks Of Celery In A Cup
Jul 03, 2025
Related Post
Thank you for visiting our website which covers about X Divided By Square Root Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.