X Is Greater Than Or Equal To 0
Kalali
May 29, 2025 · 3 min read
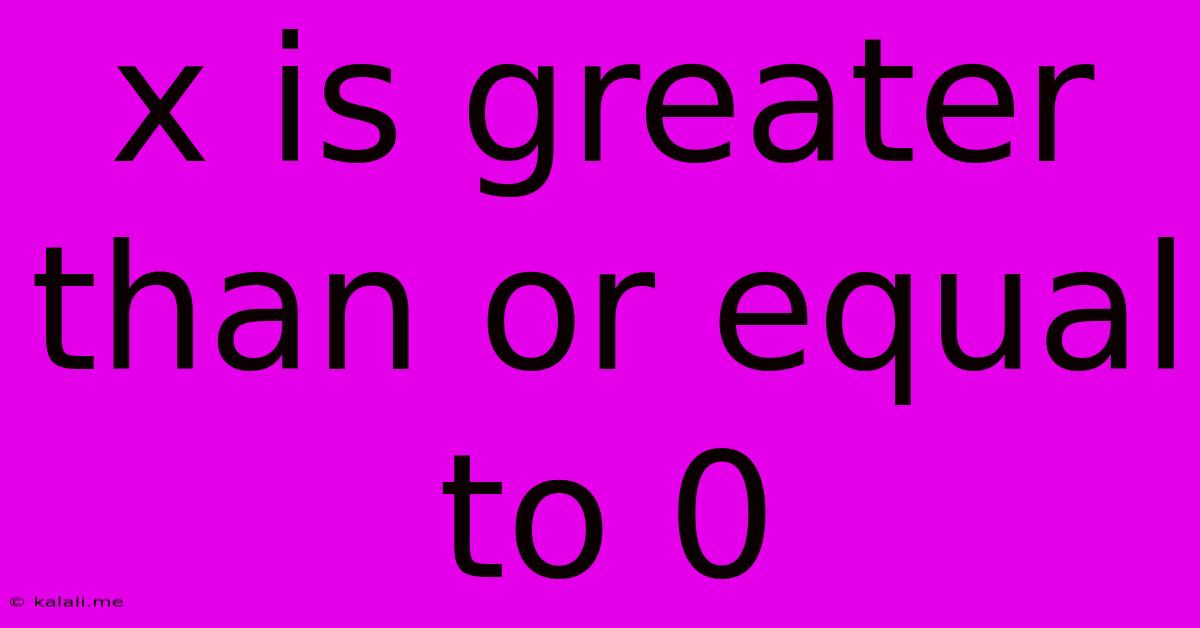
Table of Contents
Understanding "x ≥ 0": A Comprehensive Guide to Non-Negative Numbers
Meta Description: This article provides a comprehensive explanation of the mathematical inequality "x ≥ 0," covering its meaning, applications in various fields, and practical examples. Learn about non-negative numbers and their importance in real-world scenarios.
The inequality "x ≥ 0" is a fundamental concept in mathematics signifying that a variable, represented by 'x', is greater than or equal to zero. This simple statement has far-reaching implications across numerous disciplines, from basic arithmetic to advanced calculus and beyond. This article will delve into the meaning, applications, and practical implications of this inequality.
What Does x ≥ 0 Mean?
The symbol "≥" represents "greater than or equal to." Therefore, the inequality "x ≥ 0" means that the value of 'x' can be zero or any positive number. It excludes all negative numbers. This defines a set of numbers known as non-negative numbers.
This seemingly simple concept forms the basis for many mathematical operations and constraints. Understanding it is crucial for solving equations, inequalities, and interpreting data across various fields.
Applications of x ≥ 0
The constraint "x ≥ 0" frequently appears in diverse areas:
-
Real-World Quantities: Many real-world quantities cannot be negative. For example:
- Measurements: Length, weight, volume, time, and temperature are all typically non-negative. You can't have negative length or negative time.
- Counts: The number of items, people, or events is always non-negative. You can't have a negative number of apples.
- Finance: Amounts of money, profits, and assets are usually represented by non-negative numbers. A negative balance represents debt, but the amount of debt is still a positive number.
-
Mathematical Modeling: In mathematical models, this constraint is used to ensure that the solutions are physically meaningful. For instance, in models involving distances or populations, negative values are often nonsensical, so the constraint "x ≥ 0" is incorporated.
-
Linear Programming: Linear programming, an optimization technique used extensively in operations research and business, frequently uses non-negativity constraints to ensure that variables represent feasible solutions. For example, the number of products produced cannot be negative.
-
Domain Restrictions: In functions, this constraint might be used to restrict the domain. For example, a square root function is only defined for non-negative numbers. The expression √x only has real number solutions when x ≥ 0.
Examples of x ≥ 0 in Practice
Let's look at some concrete examples:
-
Solving Inequalities: If you have the inequality 2x + 1 ≥ 1, solving it yields x ≥ 0. This signifies that the solution set includes all non-negative numbers.
-
Graphing Inequalities: Graphing "x ≥ 0" on a number line would involve shading all points to the right of and including zero.
-
Domain of a Function: The function f(x) = √(x + 2) has a domain where x + 2 ≥ 0, which simplifies to x ≥ -2.
-
Real-world application: A store sells apples. The number of apples sold (x) must be greater than or equal to zero. You can't sell a negative number of apples.
Conclusion
The simple inequality "x ≥ 0" holds significant importance in various mathematical and real-world applications. Understanding its meaning and implications is vital for anyone working with mathematical models, data analysis, or any field involving quantifiable data where negative values are not meaningful. This constraint ensures realistic and interpretable results, making it a cornerstone of numerous mathematical and scientific endeavors.
Latest Posts
Latest Posts
-
Can Bulletproof Glass Be Broken By Sound
May 30, 2025
-
How To Wire Switch To Light
May 30, 2025
-
After Abstract Removed It Came Back
May 30, 2025
-
How Long Can You Ride On A Donut
May 30, 2025
-
How To Reset Oil Life Honda Accord
May 30, 2025
Related Post
Thank you for visiting our website which covers about X Is Greater Than Or Equal To 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.