X Squared + 7x + 12
Kalali
Jun 11, 2025 · 2 min read
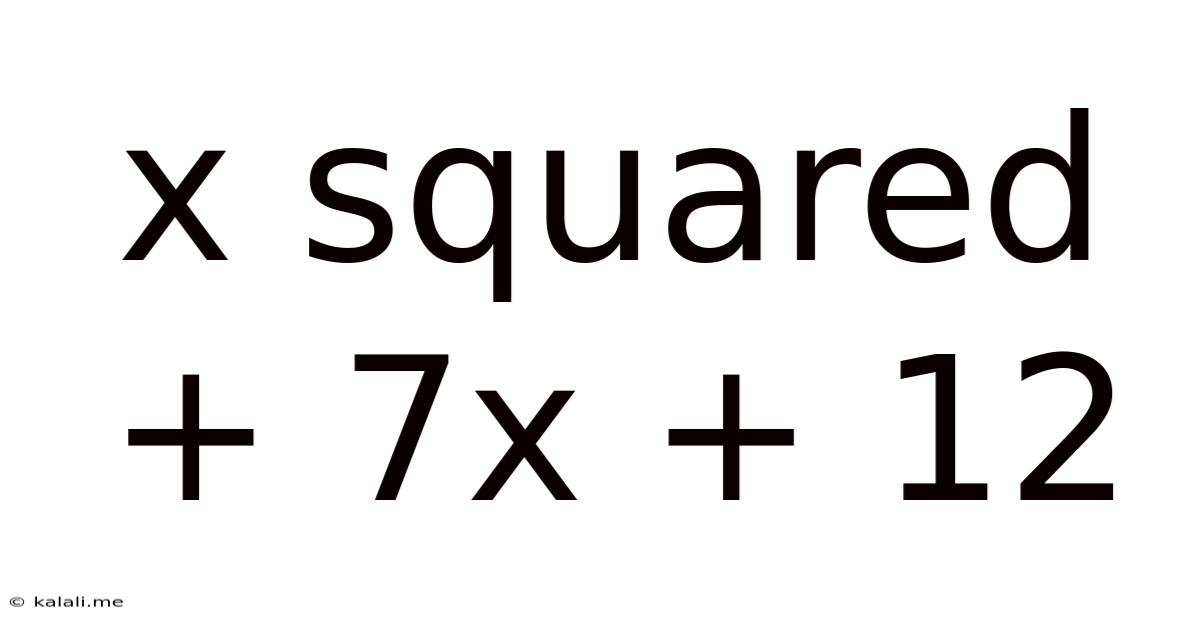
Table of Contents
Understanding the Quadratic Expression: x² + 7x + 12
This article explores the quadratic expression x² + 7x + 12, covering its factorization, solving for its roots, and its graphical representation. Understanding this seemingly simple expression provides a foundation for grasping more complex algebraic concepts. We'll delve into the methods used to manipulate and analyze this quadratic, making it accessible to both beginners and those looking for a refresher.
What is a Quadratic Expression?
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form is ax² + bx + c, where a, b, and c are constants. In our case, x² + 7x + 12, a = 1, b = 7, and c = 12.
Factorization of x² + 7x + 12
Factorization involves expressing the quadratic as a product of two linear expressions. To factor x² + 7x + 12, we look for two numbers that add up to 7 (the coefficient of x) and multiply to 12 (the constant term). These numbers are 3 and 4. Therefore, the factorization is:
(x + 3)(x + 4)
This means x² + 7x + 12 = (x + 3)(x + 4). This factored form is crucial for various applications, including solving quadratic equations and simplifying expressions.
Solving the Quadratic Equation x² + 7x + 12 = 0
Setting the quadratic expression equal to zero gives us a quadratic equation: x² + 7x + 12 = 0. Solving this equation means finding the values of x that make the equation true. Using the factored form, we can easily solve this:
(x + 3)(x + 4) = 0
This equation is true if either (x + 3) = 0 or (x + 4) = 0. Therefore, the solutions (also called roots or zeros) are:
- x = -3
- x = -4
These are the x-intercepts of the parabola represented by the quadratic equation.
Graphical Representation
The quadratic expression x² + 7x + 12 represents a parabola. Since the coefficient of x² (a) is positive, the parabola opens upwards. The vertex of the parabola, the lowest point, can be found using the formula x = -b/2a. In this case:
x = -7/(2*1) = -3.5
The y-coordinate of the vertex can be found by substituting x = -3.5 back into the original expression:
y = (-3.5)² + 7(-3.5) + 12 = -2.25
Therefore, the vertex of the parabola is (-3.5, -2.25). The parabola intersects the x-axis at x = -3 and x = -4 (the roots we found earlier).
Applications of Quadratic Expressions
Quadratic expressions and equations have numerous applications in various fields, including:
- Physics: Modeling projectile motion, calculating areas, and describing the relationship between velocity and time.
- Engineering: Designing structures, optimizing processes, and solving problems related to energy and momentum.
- Economics: Analyzing market trends, predicting consumer behavior, and maximizing profits.
Understanding the fundamentals of quadratic expressions like x² + 7x + 12 provides a strong base for tackling more advanced mathematical concepts and real-world problems. By mastering factorization, solving equations, and visualizing the graphical representation, you gain valuable tools for problem-solving across numerous disciplines.
Latest Posts
Latest Posts
-
How Many Cups Is 238 Grams Of Miralax Powder
Jul 01, 2025
-
How Much Is Half A Billion Dollars
Jul 01, 2025
-
How Many Days Are In 9 Years
Jul 01, 2025
-
How Much Is 1 8 And 1 8 Teaspoon
Jul 01, 2025
-
How Many Feet In A Quarter Acre
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about X Squared + 7x + 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.