Y 1 X 2 Z 2
Kalali
Jun 02, 2025 · 3 min read
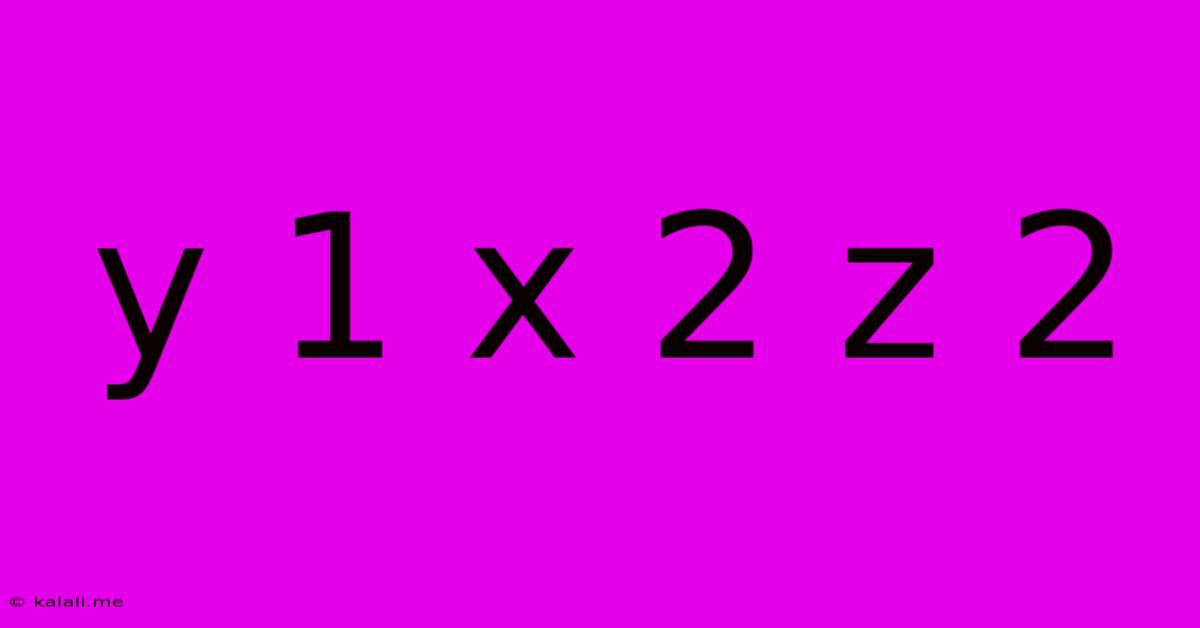
Table of Contents
Decoding the Mysterious "y = 1x² + 2z²": Exploring Quadratic Forms and Their Applications
This article delves into the mathematical expression "y = 1x² + 2z²," exploring its nature as a quadratic form, its geometrical representation, and its applications in various fields. Understanding this seemingly simple equation unlocks insights into more complex mathematical concepts and their real-world relevance. This equation, while seemingly basic, represents a fundamental building block in understanding higher-dimensional geometry and related applications.
What is a Quadratic Form?
At its core, "y = 1x² + 2z²" represents a quadratic form. A quadratic form is a homogeneous polynomial of degree two in several variables. In simpler terms, it's an expression where each term is a product of two variables, possibly the same variable (resulting in a squared term), and the highest power of any variable is two. Our example showcases a quadratic form in two variables, x and z. The coefficients (1 and 2) determine the shape and properties of the form.
Geometric Interpretation
The equation "y = x² + 2z²" can be visualized geometrically as a paraboloid. Imagine a surface in three-dimensional space where the height (y) depends on the values of x and z. The equation dictates that the surface curves upwards, creating a bowl-like shape. The coefficient of 2 in the z² term indicates that the paraboloid is steeper along the z-axis compared to the x-axis.
Applications and Extensions
Understanding quadratic forms like "y = x² + 2z²" extends far beyond basic mathematics. Their applications are widespread across numerous fields, including:
-
Physics: Quadratic forms appear frequently in physics, particularly in the description of energy systems and potential fields. For example, they can model the potential energy of a particle in certain force fields. Understanding the properties of the quadratic form helps in analyzing the particle's motion.
-
Computer Graphics: These forms are crucial in rendering 3D graphics. They are used to define surfaces and shapes, enabling the creation of realistic and complex visuals in computer games, simulations, and other applications. The coefficients of the quadratic form help in controlling the shape and curvature of these surfaces.
-
Optimization Problems: Quadratic forms play a significant role in optimization problems, a core area within mathematics and computer science. Many optimization algorithms rely on analyzing and manipulating quadratic functions to find optimal solutions. This involves finding minimum or maximum values, which are directly linked to the shape of the paraboloid representation.
-
Statistics: In multivariate statistics, quadratic forms are essential for analyzing variance-covariance matrices and understanding the relationships between multiple variables. Techniques such as principal component analysis heavily rely on the manipulation and understanding of such forms.
-
Number Theory: Quadratic forms also have deep connections to number theory, particularly in the study of Diophantine equations (equations involving integer solutions).
Expanding the Concept
The equation "y = x² + 2z²" is a simplified example. More complex quadratic forms can involve more variables and more intricate coefficient relationships. These extensions lead to higher-dimensional geometries and more challenging, but equally fascinating, mathematical explorations. The fundamental principles, however, remain the same.
This exploration provides a foundation for understanding quadratic forms and their significance. While the equation "y = x² + 2z²" might seem simple at first glance, its implications extend into many branches of mathematics and their practical applications in science and technology. Further investigation into quadratic forms and related mathematical concepts reveals a rich and rewarding field of study.
Latest Posts
Latest Posts
-
Kitchen Sink Clogged Deep In Pipe
Jun 04, 2025
-
How Many Pages Is Usually A Chapter
Jun 04, 2025
-
Can I Record A Conversation In California
Jun 04, 2025
-
The Whole Earth Will Not Be Controlled By Antichrist
Jun 04, 2025
-
How To Feed As A Vampire In Skyrim
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about Y 1 X 2 Z 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.