Z Sqrt X 2 Y 2
Kalali
Jun 01, 2025 · 3 min read
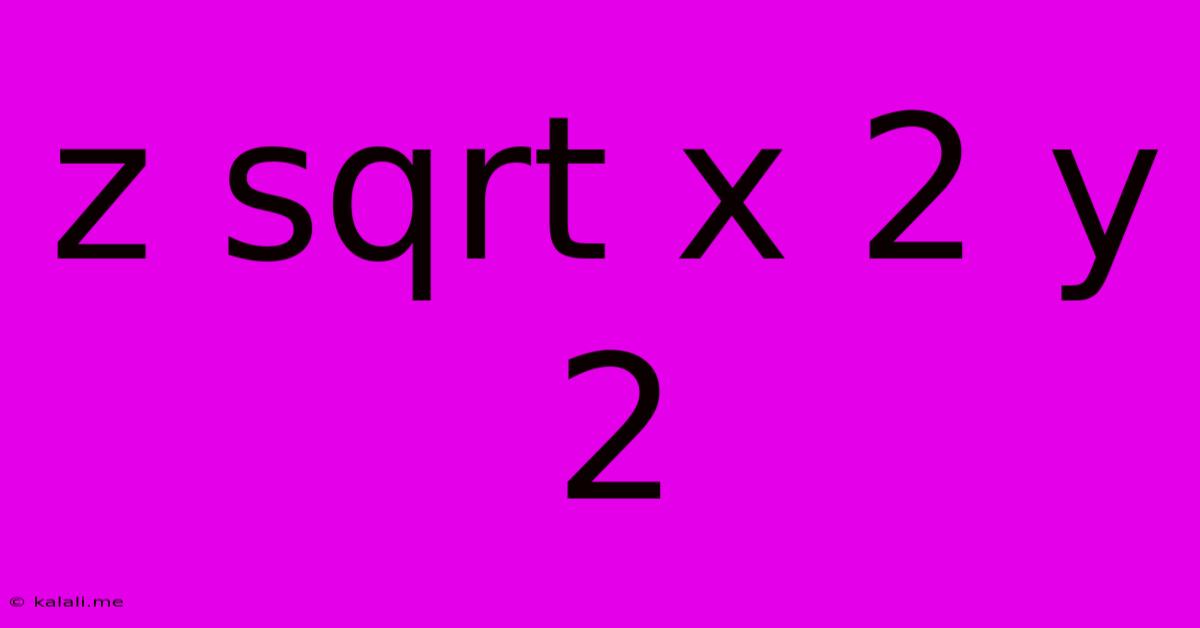
Table of Contents
Understanding the Equation: z = √(x² + y²)
This article delves into the mathematical equation z = √(x² + y²), exploring its meaning, applications, and significance in various fields. This equation represents the distance formula in two dimensions, a fundamental concept in geometry and other related disciplines. Understanding this equation is crucial for grasping concepts in coordinate geometry, vector calculus, and even physics.
What does z = √(x² + y²) represent?
The equation z = √(x² + y²) calculates the distance (z) from the origin (0,0) to a point (x,y) on a two-dimensional Cartesian plane. It's a direct application of the Pythagorean theorem. Imagine a right-angled triangle where x and y represent the lengths of the two shorter sides (legs), and z represents the length of the hypotenuse. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides (a² + b² = c²). Our equation is simply a rearrangement of this, solving for the hypotenuse (z).
Applications of the Distance Formula
This seemingly simple equation has far-reaching applications in various fields:
-
Geometry: Calculating distances between points, determining the equation of a circle, and solving geometric problems involving distances and lengths. Understanding this fundamental equation is critical for more advanced geometric concepts.
-
Computer Graphics: This formula is extensively used in computer graphics and game development to calculate distances between objects, determine collision detection, and implement realistic movements and interactions. Distance calculations are core to rendering 2D and 3D graphics.
-
Physics: Many physical phenomena rely on distance calculations. For instance, calculating the magnitude of a force vector, determining the gravitational attraction between two objects, and simulating projectile motion all involve the distance formula.
-
Data Analysis and Statistics: In data analysis, this equation is used in calculating distances between data points, which is fundamental for clustering algorithms, dimensionality reduction techniques like PCA (Principal Component Analysis), and various machine learning algorithms.
-
Navigation and Mapping: GPS systems and mapping applications heavily rely on distance calculations to determine routes, calculate travel times, and display distances between locations. Accurate distance calculations are vital for navigation software.
Visualizing the Equation
Imagine a point (x, y) on a graph. Drawing a line from the origin (0,0) to this point creates a right-angled triangle. The x-coordinate represents the horizontal distance, the y-coordinate represents the vertical distance, and the distance from the origin to the point (x, y) is calculated using the equation z = √(x² + y²). This distance, z, is always positive, as it represents a length.
Extending the Concept to Higher Dimensions
The concept of the distance formula can be extended to higher dimensions. For example, in three dimensions, the distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is given by:
d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)
This represents the extension of the Pythagorean theorem to three-dimensional space. Similar extensions can be made to even higher dimensions.
In conclusion, the equation z = √(x² + y²) is a powerful and fundamental mathematical equation with extensive applications across numerous disciplines. Understanding this equation is key to grasping more complex concepts in mathematics, computer science, physics, and other related fields. Its simplicity belies its importance in various calculations and applications involving distance and spatial relationships.
Latest Posts
Latest Posts
-
This Is Her Or This Is She
Jun 03, 2025
-
How To Change A Spiral Notebook Cover
Jun 03, 2025
-
How Do I Clean A Glass Top Stove
Jun 03, 2025
-
Mix Ratio For 0 Psi Psi
Jun 03, 2025
-
Once Upon A Time In America Ending Explained
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Z Sqrt X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.