1 1 2 1 3 1 4 1 5 1
Kalali
Jun 04, 2025 · 2 min read
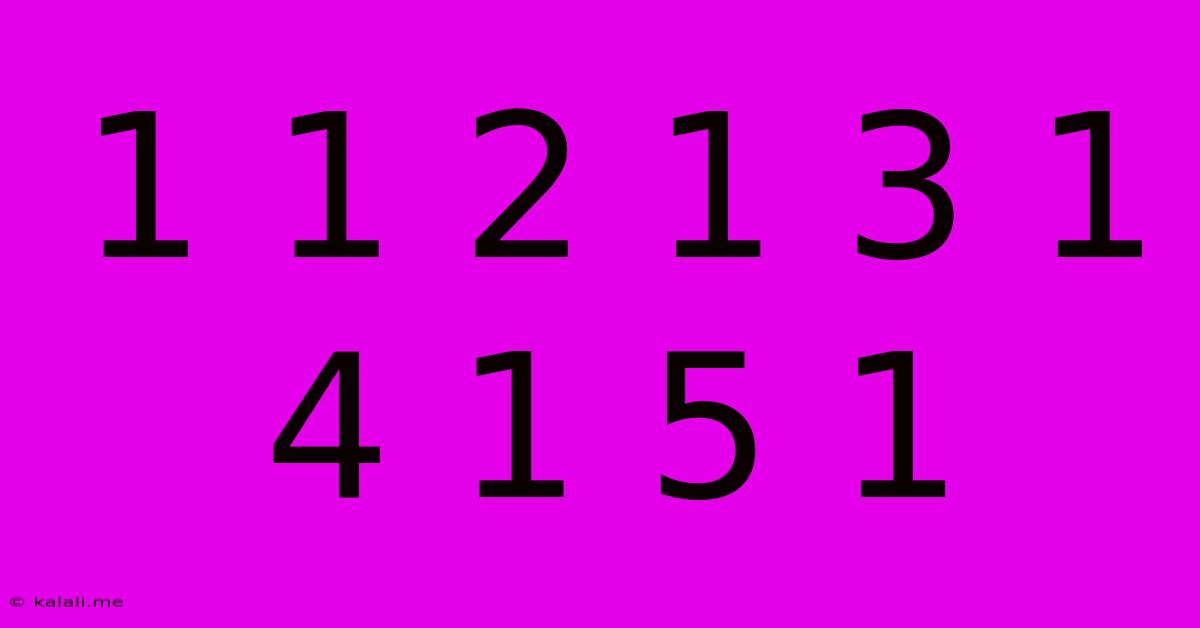
Table of Contents
Decoding the Sequence: 1 1 2 1 3 1 4 1 5 1 - A Mathematical and Pattern Exploration
This article delves into the seemingly simple numerical sequence: 1 1 2 1 3 1 4 1 5 1. While it might appear straightforward at first glance, a closer examination reveals interesting mathematical properties and potential patterns, making it a fascinating subject for exploration. Understanding the underlying structure can help us predict future elements and potentially uncover broader mathematical principles.
The sequence doesn't immediately align with commonly known mathematical progressions like arithmetic or geometric sequences. Instead, its unique structure suggests a different approach to analysis. Let's explore some possibilities.
Analyzing the Pattern: Alternating Units and Increments
A key observation is the alternating nature of the sequence. We have a consistent pattern of a "1" followed by an incrementing integer, then another "1," and so on. This suggests a possible recursive relationship or a function that generates these numbers. We can represent this pattern as:
- 1 (first element)
- 1 (second element)
- 2 (increment)
- 1 (third element)
- 3 (increment)
- 1 (fourth element)
- 4 (increment)
- 1 (fifth element)
- 5 (increment)
- 1 (sixth element)
This structure suggests that the sequence could be defined by a piecewise function or a rule involving modulo operations.
Potential Interpretations and Further Exploration
The nature of the sequence lends itself to multiple interpretations. One could consider it a simple representation of an alternating series. Another perspective might involve viewing it as a coded message, where the "1" acts as a delimiter or separator between the incrementing integers. The possibilities are numerous, and the exact meaning or purpose of the sequence might depend on the context in which it was presented.
Beyond the Sequence: Exploring Related Concepts
This exploration of the sequence 1 1 2 1 3 1 4 1 5 1 opens doors to further investigations into related mathematical concepts:
- Number Sequences and Series: This sequence serves as a simple example of a non-standard number sequence, prompting exploration of more complex patterns and their underlying rules.
- Recursive Functions and Algorithms: The alternating nature suggests a recursive definition could generate the sequence efficiently.
- Pattern Recognition: The process of identifying and defining the pattern within the sequence is a fundamental skill in mathematics and computer science.
- Data Analysis: Similar sequences might appear in various data sets; understanding this simple case can improve pattern recognition skills for more complex scenarios.
Conclusion: The Simplicity and Intrigue of 1 1 2 1 3 1 4 1 5 1
While seemingly straightforward, the sequence 1 1 2 1 3 1 4 1 5 1 presents a fascinating puzzle. Its alternating structure and potential interpretations offer opportunities for mathematical exploration, highlighting the importance of pattern recognition and the beauty of simplicity in mathematics. Further analysis could uncover additional mathematical properties or even inspire the creation of new, related sequences. The possibilities are endless, making this a sequence worthy of deeper investigation.
Latest Posts
Latest Posts
-
Can You Remove Envoys Civ 6
Jun 06, 2025
-
How To Transfer Player Inventory From World Minecraft Server
Jun 06, 2025
-
Can Pyrex Go In The Freezer
Jun 06, 2025
-
Can You Pray Fajr After Sunrise
Jun 06, 2025
-
Use A Laptop As A Monitor
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 1 3 1 4 1 5 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.