10 Is What Percent Of 25
Kalali
Apr 03, 2025 · 5 min read
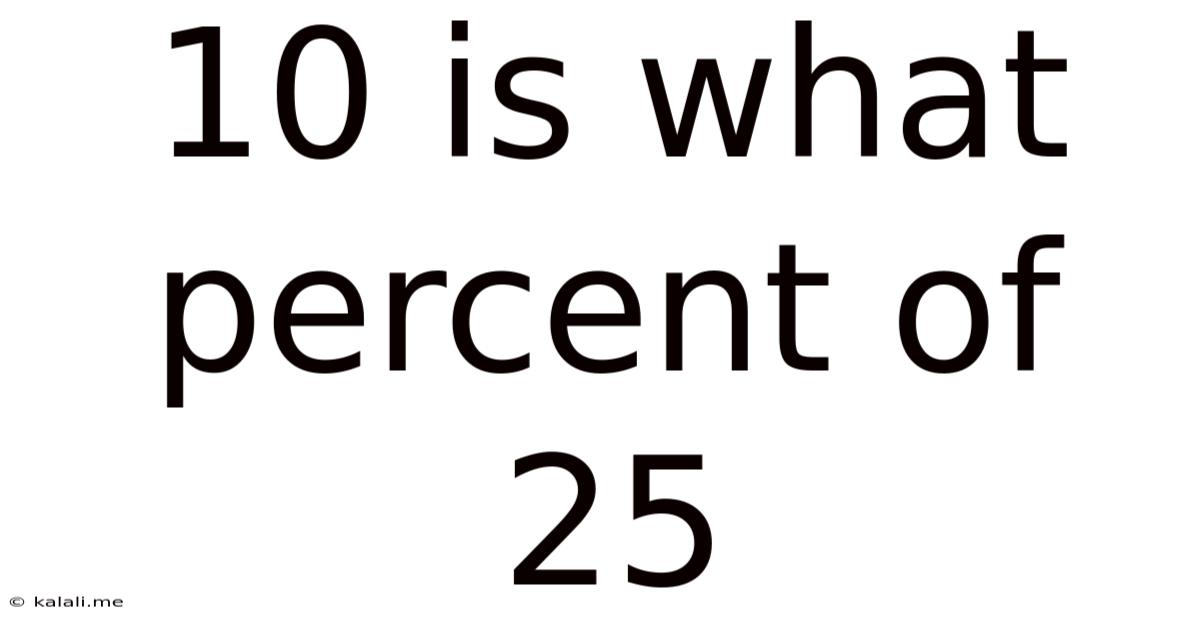
Table of Contents
10 is What Percent of 25? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article delves into the seemingly simple question, "10 is what percent of 25?", and expands it into a comprehensive exploration of percentage calculations, providing you with the tools and knowledge to confidently tackle any percentage problem you encounter.
Understanding Percentages: The Basics
Before we solve our primary question, let's establish a strong foundation in percentage concepts. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100, or as a decimal.
For example, 50% can be written as:
- Fraction: 50/100 (which simplifies to 1/2)
- Decimal: 0.50
This fundamental understanding is crucial for solving percentage problems effectively.
Calculating "10 is What Percent of 25?"
Now, let's address the core question: What percentage of 25 is 10? We can solve this using a simple formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 10
- Whole: 25
Substituting these values into the formula:
(10 / 25) * 100% = 40%
Therefore, 10 is 40% of 25.
Different Approaches to Solving Percentage Problems
While the above formula is the most straightforward, several other methods can solve percentage problems. Let's explore a few:
1. Using Proportions:
Proportions offer a visual and intuitive approach. We can set up a proportion:
10/25 = x/100
Where 'x' represents the unknown percentage. Solving for 'x' involves cross-multiplication:
25x = 1000
x = 1000 / 25
x = 40
Therefore, x = 40%, confirming our previous result.
2. Using Decimal Conversion:
We can convert the fraction (10/25) into a decimal by dividing 10 by 25:
10 / 25 = 0.4
To convert this decimal to a percentage, multiply by 100%:
0.4 * 100% = 40%
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in various real-life scenarios:
1. Retail and Sales:
Calculating discounts, sales tax, and profit margins all rely heavily on percentage calculations. For example, understanding that a 20% discount on a $100 item results in a $20 reduction is crucial for budgeting and informed purchasing decisions.
2. Finance and Investing:
Percentage calculations are fundamental in finance, from determining interest rates on loans and investments to calculating returns on investments and understanding inflation rates. Knowing how to calculate percentage changes in investment values is critical for assessing financial performance.
3. Data Analysis and Statistics:
Percentages are widely used to represent data in graphs, charts, and reports, making complex data more easily understandable. They're essential for calculating percentages of various groups within a population or analyzing the success rate of specific events.
4. Science and Research:
In scientific research, percentages are used to express experimental error, statistical significance, and the concentration of various components in a mixture. Accuracy in percentage calculations is essential for ensuring the reliability and validity of research findings.
Advanced Percentage Calculations: Finding the Whole or the Part
While the previous examples focused on finding the percentage, percentage calculations also allow us to find the whole or the part when other values are known.
1. Finding the Whole:
Let's say we know that 25% of a number is 15. To find the whole number, we can set up an equation:
0.25 * x = 15
Solving for x:
x = 15 / 0.25
x = 60
Therefore, the whole number is 60.
2. Finding the Part:
Suppose we know that 60% of a number is 30. To find the part representing 60%, we can set up an equation:
0.60 * x = 30
Solving for x:
x = 30 / 0.60
x = 50
Therefore, the whole number is 50, and the part representing 60% is 30.
Percentage Increase and Decrease Calculations
Calculating percentage increases and decreases is another important application of percentage skills.
1. Percentage Increase:
To calculate a percentage increase, we use the formula:
[(New Value - Old Value) / Old Value] * 100%
For example, if a price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
2. Percentage Decrease:
To calculate a percentage decrease, we use a similar formula:
[(Old Value - New Value) / Old Value] * 100%
If a price decreases from $60 to $50, the percentage decrease is:
[(60 - 50) / 60] * 100% ≈ 16.67%
Tips and Tricks for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use a calculator: Calculators can be helpful, especially for more complex calculations.
- Understand the formula: A strong understanding of the underlying formula will help you adapt to different problem types.
- Break down complex problems: Break down complex problems into smaller, manageable steps.
- Check your work: Always check your answers to ensure accuracy.
Conclusion: The Power of Percentages
The simple question, "10 is what percent of 25?", serves as a gateway to understanding the broader applications of percentage calculations. Mastering this fundamental skill empowers you to confidently navigate various aspects of daily life, from financial planning and shopping decisions to interpreting data and performing scientific analysis. By understanding the various methods for solving percentage problems and practicing regularly, you can unlock the power of percentages and apply this knowledge to countless real-world scenarios. Remember that consistent practice and a firm grasp of the underlying principles are key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
52 Is What Percent Of 80
Apr 04, 2025
-
How Many Seconds In 35 Minutes
Apr 04, 2025
-
What Is 4 As A Fraction
Apr 04, 2025
-
What Percent Is 12 Of 50
Apr 04, 2025
-
Which Discovery Supported The Endosymbiotic Theory
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 10 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
