10 Out Of 16 As A Percentage
Kalali
Apr 09, 2025 · 5 min read
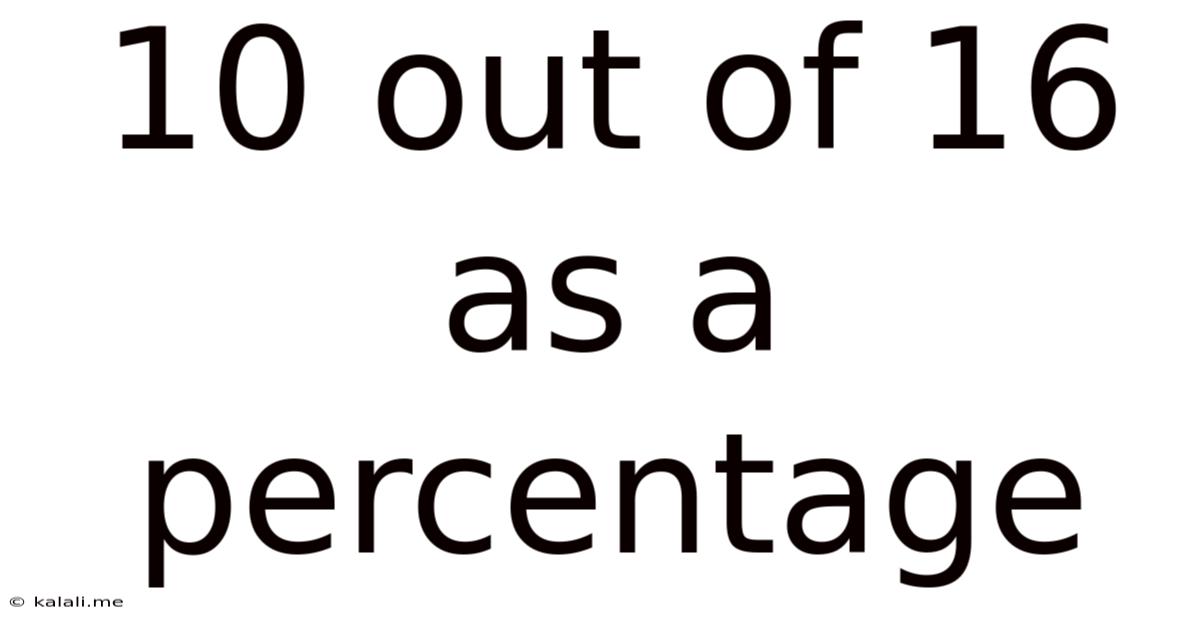
Table of Contents
10 Out of 16 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in a store to analyzing financial reports. This article delves deep into how to calculate 10 out of 16 as a percentage, and more broadly, how to master percentage calculations. We'll cover the core concepts, explore different calculation methods, provide real-world examples, and even touch upon advanced applications. By the end, you'll not only know the answer to "10 out of 16 as a percentage" but also possess the confidence to tackle any percentage problem.
What is a Percentage?
Before we dive into the specifics, let's solidify our understanding of what a percentage actually represents. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" signifies "percent" or "out of 100". For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Percentages are incredibly useful for representing proportions, making comparisons easier, and illustrating changes over time.
Calculating 10 Out of 16 as a Percentage: The Basic Method
The most straightforward way to calculate 10 out of 16 as a percentage involves these three simple steps:
-
Form a fraction: Express the problem as a fraction. In this case, it's 10/16. This represents the part (10) over the whole (16).
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (16). 10 ÷ 16 = 0.625
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.625 x 100 = 62.5%
Therefore, 10 out of 16 is 62.5%.
Alternative Calculation Methods
While the above method is the most common, there are alternative approaches you can use, especially helpful if you're working with more complex scenarios or prefer mental calculations:
-
Using Proportions: You can set up a proportion: 10/16 = x/100. Solving for x will give you the percentage. Cross-multiply: 16x = 1000. Divide both sides by 16: x = 62.5.
-
Simplifying the Fraction First: Before converting to a decimal, you can simplify the fraction 10/16 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2. This simplifies the fraction to 5/8. Then, divide 5 by 8 (0.625) and multiply by 100 to get 62.5%. Simplifying first can make the division easier.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives. Here are some examples:
-
Discounts and Sales: A common use of percentages is calculating discounts. If a store offers a 20% discount on a $100 item, the discount is 20% of $100, which is $20. The final price would be $80.
-
Taxes and Interest: Calculating sales tax, income tax, or interest on loans all involve percentages. For instance, if the sales tax is 6%, you would multiply the price of an item by 0.06 to find the tax amount.
-
Grades and Performance: Percentages are widely used to represent academic performance. A score of 85% on a test means you answered 85 out of 100 questions correctly.
-
Statistics and Data Analysis: Percentages are crucial for analyzing data and representing proportions within a population. For example, expressing the percentage of people who prefer a particular product.
-
Financial Investments: Understanding percentage changes in stock prices, investment returns, and interest rates is essential for financial planning and investment decisions. Calculating percentage increases or decreases helps track investment performance.
-
Scientific Experiments and Research: Percentages are used to represent the success rate of experiments, the effectiveness of treatments, and to analyze data from various scientific studies. For example, the success rate of a new drug or the percentage of participants showing positive results.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond simple percentage calculations, understanding percentage increases and decreases is crucial for more complex scenarios.
Percentage Increase: To calculate a percentage increase, follow these steps:
- Find the difference between the new value and the original value.
- Divide the difference by the original value.
- Multiply the result by 100 to express it as a percentage.
Percentage Decrease: The process for calculating a percentage decrease is very similar:
- Find the difference between the original value and the new value.
- Divide the difference by the original value.
- Multiply the result by 100 to express it as a percentage.
Example: If the price of a product increased from $50 to $60, the percentage increase is calculated as follows:
- Difference: $60 - $50 = $10
- Divide by original value: $10 / $50 = 0.2
- Multiply by 100: 0.2 x 100 = 20%
Therefore, the price increased by 20%.
Common Mistakes to Avoid When Calculating Percentages
Even though percentage calculations are relatively straightforward, some common errors can lead to incorrect results:
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Confusing Percentage Increase/Decrease: Remember to correctly identify the original and new values when calculating percentage changes. The original value is always the denominator.
-
Misinterpreting the Question: Carefully read and understand the problem statement before attempting to solve it. Ensure you're calculating the correct percentage.
-
Rounding Errors: Be mindful of rounding errors, especially when working with multiple decimal places. Rounding too early can lead to inaccuracies.
-
Not Converting to Decimal: Remember to convert percentages to decimals (by dividing by 100) before performing calculations involving multiplication or division.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a valuable skill applicable across numerous fields. We’ve covered the fundamentals, explored different methods for calculating 10 out of 16 as a percentage (which is 62.5%), and delved into real-world applications and advanced techniques. By avoiding common mistakes and practicing regularly, you'll become proficient in percentage calculations and confidently apply this skill to various situations, improving your analytical abilities and problem-solving skills. Remember, practice is key to mastery! Try different examples and apply your knowledge to real-life scenarios to solidify your understanding. The more you practice, the easier and more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
7 Is What Percent Of 8
Apr 17, 2025
-
2 1 4 As An Improper Fraction
Apr 17, 2025
-
65 Cm Equals How Many Inches
Apr 17, 2025
-
What Is 100 In Decimal Form
Apr 17, 2025
-
What Is 60 As A Fraction
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 16 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.