100 Is What Percent Of 500
Kalali
Apr 27, 2025 · 5 min read
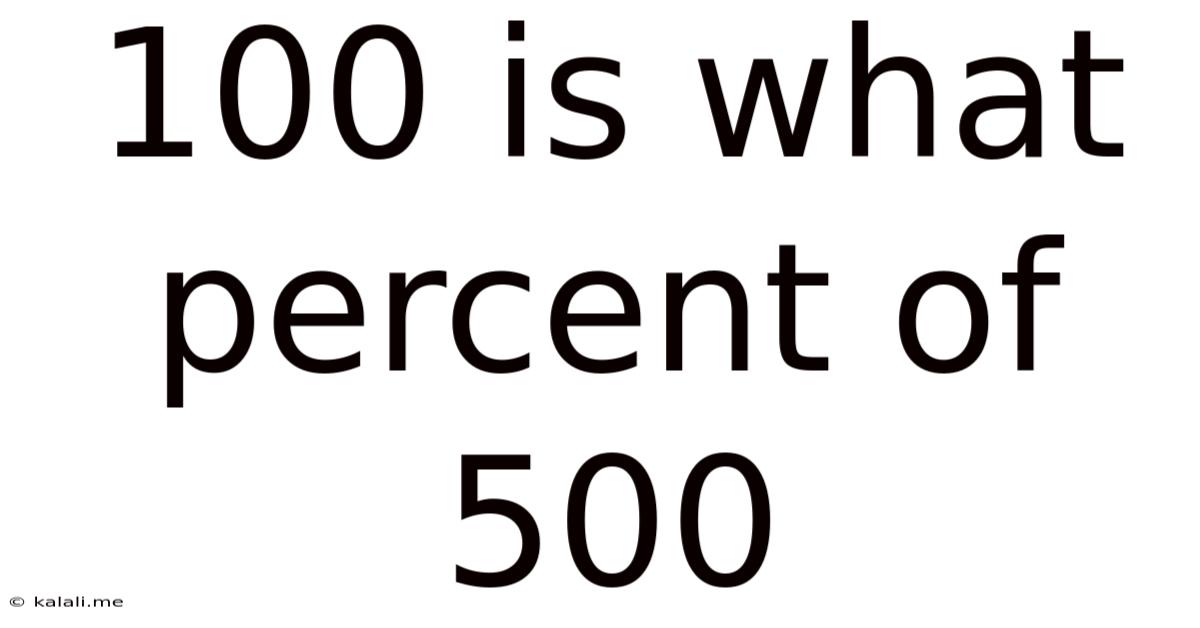
Table of Contents
100 is What Percent of 500: A Comprehensive Guide to Percentage Calculations
This article will delve into the seemingly simple question: "100 is what percent of 500?" While the answer might seem readily apparent, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting to complex financial modeling. We'll explore the solution methodically, examining the formula, applying it to this specific problem, and then expanding on the broader context of percentage calculations, providing practical examples and tips for mastering this essential mathematical skill. This comprehensive guide will equip you with the knowledge and confidence to tackle any percentage problem.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Understanding this foundational concept is key to solving percentage problems. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
The Percentage Formula: The Key to Solving Problems
The core formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
- Part: This represents the specific value you're interested in expressing as a percentage of the whole. In our example, the part is 100.
- Whole: This is the total value, the complete amount that the part is a portion of. In our case, the whole is 500.
- Percentage: This is the result of the calculation, expressed as a percentage.
Solving the Problem: 100 is What Percent of 500?
Now, let's apply the formula to answer our question:
-
Identify the Part and the Whole:
- Part = 100
- Whole = 500
-
Apply the Formula:
(100 / 500) * 100% = Percentage
-
Calculate the Result:
(0.2) * 100% = 20%
Therefore, 100 is 20% of 500.
Beyond the Basics: Variations and Applications
While the above example is straightforward, understanding how to manipulate the formula allows you to solve a wider range of percentage problems. Let's explore some variations:
1. Finding the Part:
If you know the percentage and the whole, you can find the part using this modified formula:
(Percentage / 100%) * Whole = Part
For example: What is 30% of 800?
(30% / 100%) * 800 = 240
2. Finding the Whole:
If you know the percentage and the part, you can find the whole using this modified formula:
(Part / Percentage%) * 100% = Whole
For example: 150 is 25% of what number?
(150 / 25%) * 100% = 600
Real-World Applications of Percentage Calculations:
Percentage calculations are essential in many aspects of life:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Shopping: Determining sale prices, comparing deals, and understanding value for money.
- Science: Expressing experimental results, analyzing data, and representing proportions.
- Statistics: Analyzing data sets, understanding probabilities, and presenting findings.
- Everyday Life: Calculating tips, splitting bills, and understanding proportions in recipes.
Practical Examples:
Let's look at some real-world scenarios where percentage calculations are critical:
-
Calculating a Discount: A store offers a 20% discount on a $150 item. The discount amount is (20%/100%) * $150 = $30. The final price is $150 - $30 = $120.
-
Determining Sales Tax: A state has a 6% sales tax. You buy an item for $50. The sales tax is (6%/100%) * $50 = $3. The total cost is $50 + $3 = $53.
-
Calculating a Tip: You want to leave a 15% tip on a $75 dinner bill. The tip amount is (15%/100%) * $75 = $11.25.
-
Understanding Investment Returns: Your investment grew by 10% this year. If your initial investment was $1000, your profit is (10%/100%) * $1000 = $100. Your total investment is now $1100.
-
Analyzing Survey Results: In a survey of 200 people, 60% preferred option A. The number of people who preferred option A is (60%/100%) * 200 = 120.
Tips for Mastering Percentage Calculations:
- Practice Regularly: The more you practice, the more comfortable you'll become with the formulas and the application of percentages.
- Use Online Calculators: While understanding the underlying principles is crucial, using online calculators for complex calculations can be beneficial.
- Break Down Complex Problems: Large problems can be broken down into smaller, more manageable steps.
- Check Your Work: Always verify your answers to avoid errors.
- Understand the Context: The most important aspect is to correctly identify the "part" and the "whole" within the problem's context.
Advanced Percentage Concepts:
Beyond the basic calculations, several advanced concepts build upon the foundation we’ve established:
-
Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%. A positive result indicates an increase, while a negative result indicates a decrease.
-
Percentage Points: This is a critical distinction. It represents the absolute difference between two percentages. For example, if a percentage increases from 10% to 15%, the increase is 5 percentage points, not 50%.
-
Compound Interest: This involves earning interest on both the principal amount and accumulated interest. It's crucial for understanding long-term investments and loan repayments.
-
Percentage Yield: In financial contexts, this relates the actual return on an investment to the initial investment.
Conclusion:
Understanding percentage calculations is a fundamental skill applicable across numerous fields. While the question "100 is what percent of 500?" provides a simple starting point, mastering the underlying principles allows you to solve a wide array of problems confidently and accurately. By consistently practicing and applying these concepts, you'll develop a robust understanding of percentages, making them a valuable tool in both personal and professional endeavors. Remember to always clearly identify the part and the whole to avoid confusion and ensure accurate calculations. With practice and a good understanding of the formulas, you'll become proficient in calculating percentages and applying this knowledge to a variety of real-world situations.
Latest Posts
Latest Posts
-
What Percent Of 10 Is 9
Apr 27, 2025
-
How Do Limiting Factors Affect Organisms In A Community
Apr 27, 2025
-
What Is 54 Inches In Centimeters
Apr 27, 2025
-
How Many Ounces Is 1 4 Pound
Apr 27, 2025
-
How Many Inches In 81 Cm
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 100 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.