What Percent Of 10 Is 9
Kalali
Apr 27, 2025 · 5 min read
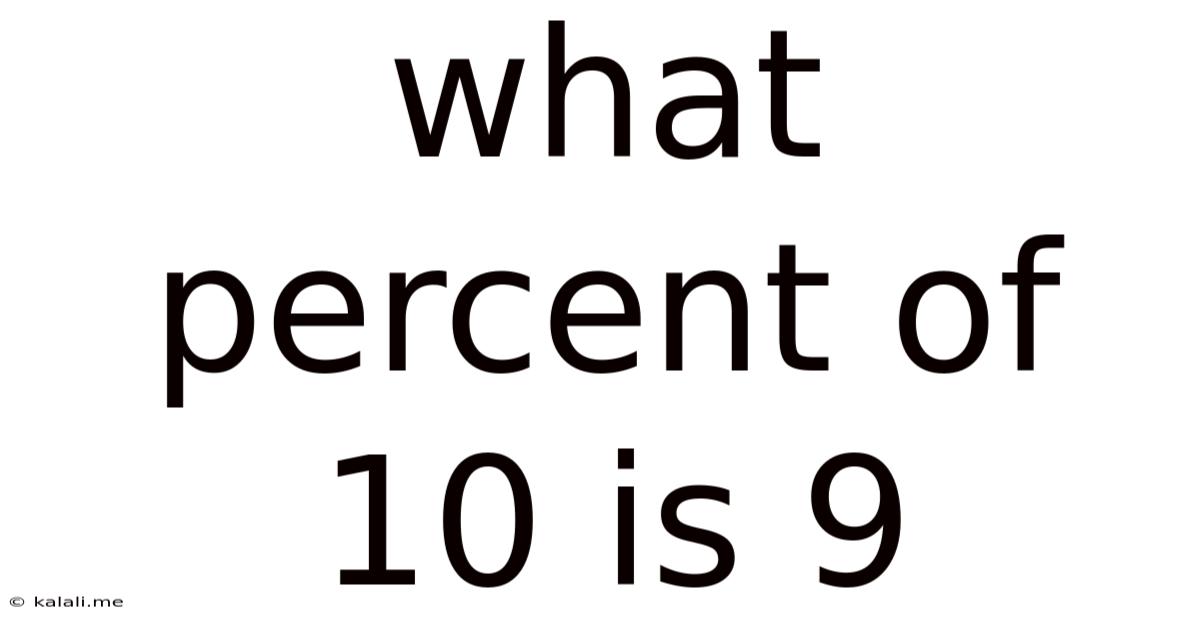
Table of Contents
What Percent of 10 is 9? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent of 10 is 9?" – opens the door to a broader understanding of percentage calculations, their applications in various fields, and the underlying mathematical principles. While the answer itself is straightforward, exploring the how and why reveals valuable insights applicable to more complex percentage problems. This article will not only answer the question directly but also delve into the methods used, explore different approaches to solving similar problems, and highlight real-world applications of percentage calculations.
Meta Description: Discover how to calculate percentages with a detailed explanation of finding what percent of 10 is 9. Learn various methods, explore real-world applications, and master percentage calculations for everyday use.
Understanding Percentages:
Percentages are a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is crucial for tackling any percentage problem.
Method 1: Using the Percentage Formula
The most common way to solve percentage problems is using the basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 9 (the number we want to express as a percentage)
- Whole: 10 (the total amount)
Plugging these values into the formula:
(9 / 10) * 100 = 90
Therefore, 9 is 90% of 10.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve our problem:
9/10 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we can cross-multiply:
10x = 900
x = 900 / 10
x = 90
Again, we arrive at the answer: 9 is 90% of 10.
Method 3: Using Decimal Equivalents
Percentages can be easily converted to decimals by dividing by 100. Conversely, decimals can be converted to percentages by multiplying by 100. This method offers a slightly different approach:
First, express the part as a fraction of the whole: 9/10 = 0.9
Then, convert the decimal to a percentage by multiplying by 100: 0.9 * 100 = 90%
Real-World Applications of Percentage Calculations:
Percentage calculations are ubiquitous in everyday life, impacting various aspects of our personal and professional lives. Here are a few examples:
-
Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $50 item means a savings of $10 (20% of $50).
-
Taxes and Interest: Taxes, such as sales tax or income tax, are often calculated as a percentage of the total amount. Similarly, interest on loans or savings accounts is usually expressed as a percentage rate.
-
Grades and Scores: Academic grades are often represented as percentages, indicating the proportion of correct answers or the overall performance in a course.
-
Statistics and Data Analysis: Percentages play a vital role in presenting and interpreting statistical data. For instance, market share, survey results, and population demographics are frequently expressed as percentages.
-
Financial Investments: Return on investment (ROI) is a crucial metric in finance, often expressed as a percentage to gauge the profitability of an investment.
-
Scientific Measurements: In scientific fields, percentages are used to express concentrations, error margins, and changes in various measurements.
Solving More Complex Percentage Problems:
While the initial problem was straightforward, understanding the underlying principles allows us to tackle more complex percentage questions. Consider these examples:
-
Finding the Whole: If 25% of a number is 15, what is the number?
We can set up the equation: 0.25 * x = 15. Solving for x, we find x = 60.
-
Finding the Part: What is 35% of 80?
This can be solved as: 0.35 * 80 = 28.
-
Finding the Percentage Increase or Decrease: A product's price increased from $50 to $60. What is the percentage increase?
First, find the difference: $60 - $50 = $10. Then, divide the difference by the original price and multiply by 100: ($10 / $50) * 100 = 20%. The price increased by 20%.
-
Compound Interest: Calculating compound interest involves applying the percentage increase multiple times over a period. This requires a more advanced formula involving exponents, but the underlying concept remains the same - a repeated application of percentage calculations.
Mastering Percentage Calculations:
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. The key is to break down the problem into its component parts – identifying the "part," the "whole," and the unknown variable – and then applying the appropriate formula or method. Consistent practice with various problem types will build confidence and proficiency in solving percentage problems of any complexity.
Beyond the Basics: Advanced Percentage Concepts:
The world of percentages extends beyond basic calculations. More advanced concepts include:
-
Percentage Points: A percentage point represents an absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted Averages: When calculating averages with different weights assigned to each component, percentages play a key role in determining the overall weighted average.
-
Percentage Change: Calculating the percentage change between two values provides insights into growth or decline. This is particularly useful in analyzing trends and making comparisons over time.
In conclusion, the seemingly simple question of "What percent of 10 is 9?" serves as a gateway to understanding a powerful and widely applicable mathematical concept. By mastering percentage calculations, you equip yourself with a valuable skill applicable across numerous fields, enabling you to analyze data, make informed decisions, and navigate various real-world scenarios with confidence. The more you practice, the more comfortable and proficient you'll become in tackling these essential calculations.
Latest Posts
Latest Posts
-
What Is The Percentage Of 0 1
Apr 28, 2025
-
What Is 0 02 As A Percent
Apr 28, 2025
-
How Many Feet Is 178 Inches
Apr 28, 2025
-
What Is 0 03 As A Fraction
Apr 28, 2025
-
What Percent Is 4 Out Of 6
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.