11 6 As A Mixed Number
Kalali
Apr 17, 2025 · 5 min read
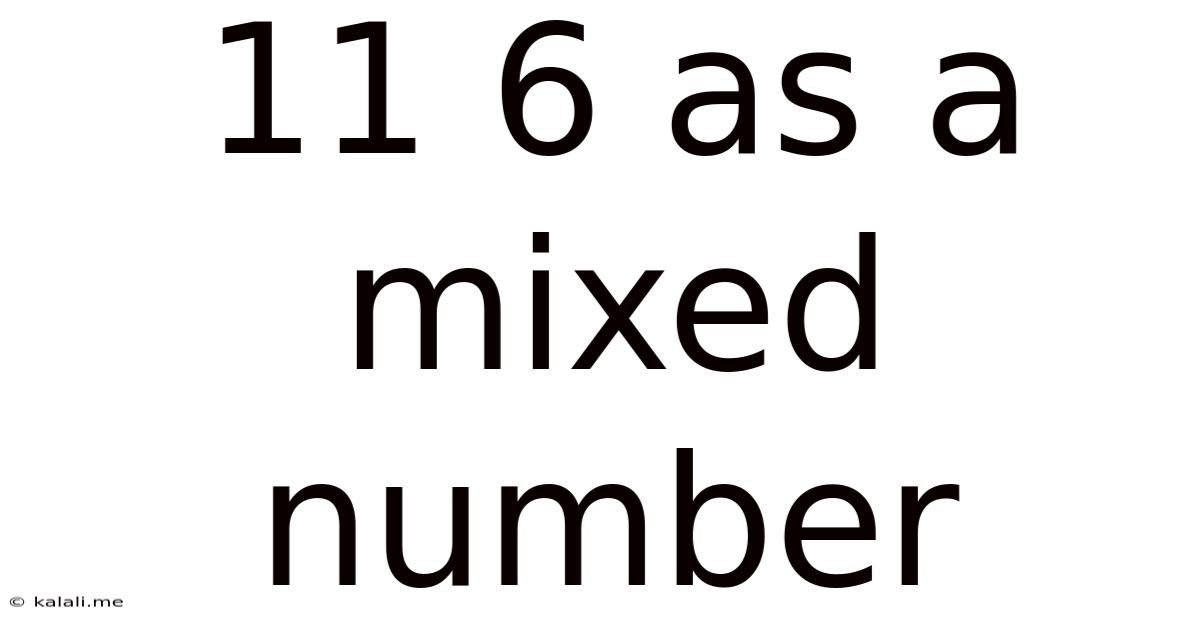
Table of Contents
Understanding 11/6 as a Mixed Number: A Comprehensive Guide
Meta Description: Learn how to convert the improper fraction 11/6 into a mixed number. This comprehensive guide explains the process step-by-step, including visual aids and practice problems, ensuring you master this fundamental math concept. We also explore the real-world applications of mixed numbers and their importance in various fields.
Converting improper fractions to mixed numbers is a fundamental skill in mathematics, crucial for understanding fractions and their applications in various fields. This article provides a thorough explanation of how to convert the improper fraction 11/6 into a mixed number, covering the process, its practical applications, and related concepts. We will explore the concept in depth, ensuring you gain a solid understanding of this important mathematical operation.
What is an Improper Fraction?
Before diving into the conversion, let's clarify what an improper fraction is. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). In our case, 11/6 is an improper fraction because 11 (the numerator) is greater than 6 (the denominator). Improper fractions represent a value greater than or equal to one.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator. Mixed numbers offer a more intuitive way to represent quantities greater than one. For example, 1 ½ represents one whole unit and half of another unit.
Converting 11/6 to a Mixed Number: A Step-by-Step Guide
The conversion process involves dividing the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same. Let's break down the conversion of 11/6:
-
Divide the numerator by the denominator: We divide 11 by 6. 11 ÷ 6 = 1 with a remainder of 5.
-
Identify the whole number: The quotient, 1, becomes the whole number part of our mixed number.
-
Identify the new numerator: The remainder, 5, becomes the numerator of the fractional part.
-
Retain the denominator: The denominator remains 6.
Therefore, 11/6 converted to a mixed number is 1 ⁵⁄₆.
Visual Representation of 11/6
Imagine you have 11 slices of pizza, and each pizza has 6 slices. You can make one complete pizza (6 slices) and have 5 slices left over. This visually represents the mixed number 1 ⁵⁄₆.
Practice Problems: Converting Improper Fractions to Mixed Numbers
Let's solidify your understanding with a few practice problems:
-
Convert 7/4 to a mixed number: 7 ÷ 4 = 1 with a remainder of 3. Therefore, 7/4 = 1 ¾.
-
Convert 13/5 to a mixed number: 13 ÷ 5 = 2 with a remainder of 3. Therefore, 13/5 = 2 ⅗.
-
Convert 22/7 to a mixed number: 22 ÷ 7 = 3 with a remainder of 1. Therefore, 22/7 = 3 ¹⁄₇.
Converting Mixed Numbers to Improper Fractions: The Reverse Process
It's equally important to understand the reverse process: converting a mixed number back to an improper fraction. This is often required in calculations involving fractions. Let's use our example, 1 ⁵⁄₆:
-
Multiply the whole number by the denominator: 1 x 6 = 6
-
Add the numerator: 6 + 5 = 11
-
Retain the denominator: The denominator remains 6.
Therefore, 1 ⁵⁄₆ converts back to the improper fraction 11/6.
Real-World Applications of Mixed Numbers
Mixed numbers are not just abstract mathematical concepts; they have numerous practical applications in everyday life and various professions:
-
Cooking and Baking: Recipes often use mixed numbers to specify quantities of ingredients, such as 2 ½ cups of flour or 1 ¾ teaspoons of baking powder.
-
Measurement: Measuring lengths, weights, and volumes frequently involves mixed numbers. For example, a board might measure 3 ⅛ feet long, or a container might hold 1 ½ gallons of liquid.
-
Construction and Engineering: Precision in construction and engineering projects necessitates the use of mixed numbers for accurate measurements and calculations.
-
Data Analysis: Statistical data might be represented using mixed numbers, particularly when dealing with averages or proportions.
-
Time: Telling time utilizes mixed numbers implicitly. For example, 2:30 represents two and a half hours.
Importance of Mastering Fraction Conversion
Proficiency in converting between improper fractions and mixed numbers is essential for various reasons:
-
Simplification: Mixed numbers often provide a clearer and more intuitive representation of quantities than improper fractions, making them easier to understand and work with.
-
Problem Solving: Many mathematical problems require converting between these forms to simplify calculations and reach a solution.
-
Real-World Applications: As discussed above, understanding mixed numbers is crucial for handling real-world situations involving measurements, quantities, and proportions.
-
Foundation for Advanced Math: This skill forms a solid foundation for more advanced mathematical concepts, such as algebra and calculus.
Advanced Concepts: Working with Mixed Numbers in Equations
Once you've mastered the basic conversion, you can apply this knowledge to more complex mathematical operations. For instance, adding, subtracting, multiplying, and dividing mixed numbers requires converting them to improper fractions first for easier calculation.
Adding Mixed Numbers:
To add mixed numbers, first convert them to improper fractions, then find a common denominator, add the numerators, and simplify the result back to a mixed number if necessary.
Subtracting Mixed Numbers:
Similar to addition, subtract mixed numbers by first converting them to improper fractions, finding a common denominator, subtracting the numerators, and simplifying the result.
Multiplying Mixed Numbers:
Convert mixed numbers to improper fractions, then multiply the numerators and denominators. Simplify the result to its lowest terms and convert back to a mixed number if needed.
Dividing Mixed Numbers:
Convert mixed numbers to improper fractions, then invert the second fraction (reciprocal) and multiply. Simplify the result as needed.
Conclusion
Understanding how to convert 11/6 to a mixed number, and more generally, how to convert between improper fractions and mixed numbers, is a cornerstone of mathematical literacy. This skill is not only crucial for academic success but also essential for navigating various aspects of everyday life and professional fields. By mastering this fundamental concept and understanding its applications, you equip yourself with a valuable tool for problem-solving and numerical understanding. Practice makes perfect, so continue practicing these conversions to solidify your understanding and build confidence in your mathematical abilities. Remember to always check your work to ensure accuracy and precision.
Latest Posts
Latest Posts
-
What Are The Factors Of 68
Apr 19, 2025
-
What Is 10 Percent Of 150
Apr 19, 2025
-
How Tall Is 54 Inches In Height
Apr 19, 2025
-
How Many Seconds Is 7 Hours
Apr 19, 2025
-
How Many Pounds Are 5 Kg
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 11 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.