12 Of 15 Is What Percent
Kalali
Apr 14, 2025 · 5 min read
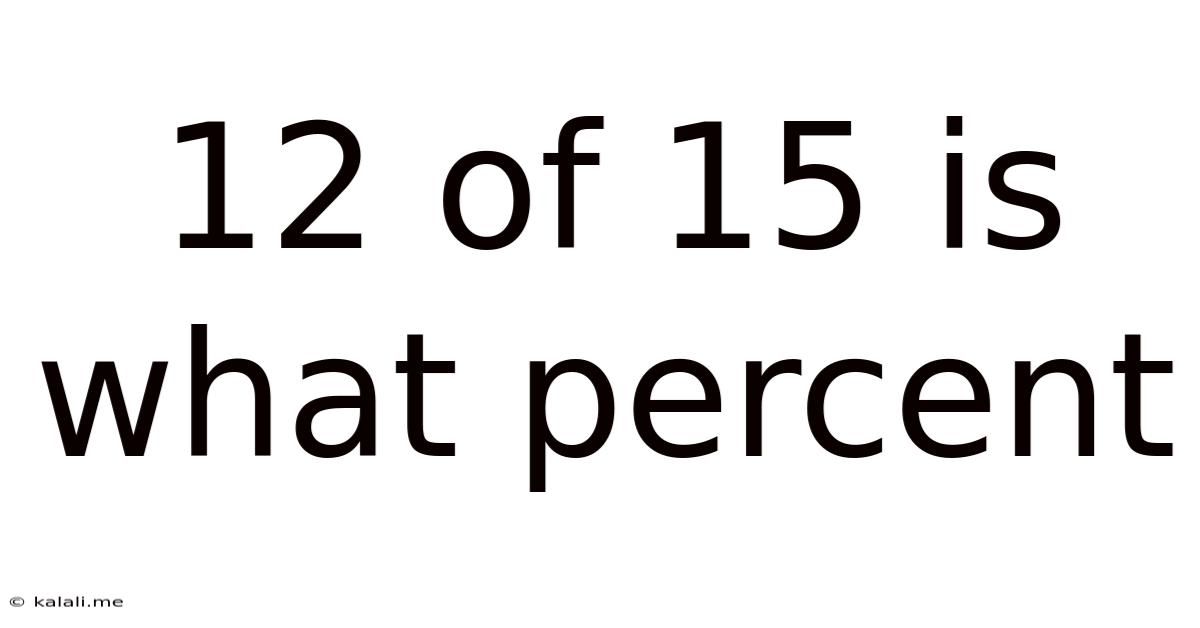
Table of Contents
12 out of 15 is What Percent? A Deep Dive into Percentage Calculations and Real-World Applications
Meta Description: Learn how to calculate percentages, understand the concept of ratios, and explore real-world applications of percentage calculations, all illustrated with the example of determining what percentage 12 out of 15 represents. This guide covers basic to advanced techniques.
Finding the percentage that 12 out of 15 represents is a fundamental percentage problem. While the answer is easily obtainable with a calculator, understanding the underlying process is crucial for tackling more complex percentage calculations and applying this knowledge across various fields. This article will not only show you how to calculate 12 out of 15 as a percentage but also explore the underlying concepts, alternative calculation methods, and practical applications of percentage calculations in everyday life.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Essentially, a percentage represents a portion of a whole. Understanding this foundational concept is key to mastering percentage calculations.
For instance, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5. Similarly, 25% represents 25 out of 100, simplifying to 1/4 or 0.25. This representation allows for easy comparison and understanding of proportions.
Calculating 12 out of 15 as a Percentage: The Direct Method
The most straightforward way to calculate the percentage is using a simple formula:
(Part / Whole) * 100%
In this case:
- Part: 12 (the number we're considering as a portion of the whole)
- Whole: 15 (the total number representing the complete set)
Applying the formula:
(12 / 15) * 100% = 0.8 * 100% = 80%
Therefore, 12 out of 15 is 80%.
Alternative Calculation Methods
While the direct method is efficient, alternative methods can enhance understanding and provide flexibility, particularly with more complex problems.
Method 2: Using Proportions
We can set up a proportion to solve this:
12/15 = x/100
Cross-multiplying, we get:
15x = 1200
Dividing both sides by 15:
x = 80
Therefore, x = 80%, confirming our previous result. This method is useful for visualizing the relationship between the parts and the whole.
Method 3: Simplifying the Fraction
Before multiplying by 100%, we can simplify the fraction 12/15:
12/15 simplifies to 4/5
Now, we can calculate the percentage:
(4/5) * 100% = 0.8 * 100% = 80%
This method demonstrates the importance of simplifying fractions to make calculations easier and reduces the risk of errors with larger numbers.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional settings. Here are a few examples:
1. Finance and Budgeting:
- Calculating interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Determining discounts and sales tax: Retail stores use percentages to advertise discounts and calculate sales tax on purchases. Understanding these calculations helps consumers make informed buying decisions.
- Analyzing investment returns: Investors use percentages to track the performance of their investments and assess profitability.
2. Science and Statistics:
- Expressing experimental results: Scientists often express their findings as percentages, for example, the percentage of a population affected by a certain disease or the percentage of successful trials in an experiment. This allows for clear and concise communication of data.
- Data analysis and representation: Percentages are frequently used in data visualization and representation, such as in pie charts and bar graphs, making complex data easier to understand. Statistical significance is often expressed using percentages.
3. Education and Grading:
- Calculating grades: Teachers use percentages to assign final grades based on student performance on assignments, tests, and projects.
- Tracking student progress: Educational institutions use percentages to monitor the academic progress of students and identify areas needing improvement.
4. Everyday Life:
- Calculating tips: Diners use percentages to calculate tips for restaurant service.
- Determining nutritional information: Food labels often express nutritional information such as fat and protein content as percentages of the recommended daily intake.
- Understanding surveys and polls: Surveys and polls often present results in percentage form, showing the proportion of respondents holding a particular view.
Beyond the Basics: Handling More Complex Percentage Problems
The example of 12 out of 15 is relatively straightforward. However, understanding the underlying principles allows you to tackle more complex scenarios:
1. Finding the Percentage Increase or Decrease:
Calculating the percentage change between two values requires understanding the difference and relating it to the original value. For example, if a price increases from $10 to $12, the percentage increase is calculated as:
((12 - 10) / 10) * 100% = 20%
2. Calculating Percentage Points:
Percentage points represent the arithmetic difference between two percentages, not the percentage difference. For instance, an increase from 10% to 15% is a 5-percentage-point increase, but a 50% increase relative to the initial 10%.
3. Working with Multiple Percentages:
Problems involving multiple percentages, such as successive discounts or compounded interest, require a step-by-step approach. You cannot simply add or subtract the percentages directly. For example, a 20% discount followed by a 10% discount is not equivalent to a 30% discount.
Conclusion: Mastering Percentages for a Data-Driven World
Understanding how to calculate percentages, as demonstrated by the example of determining what percentage 12 out of 15 represents, is a crucial skill with broad applications. From everyday budgeting to complex financial analysis and scientific research, the ability to work confidently with percentages empowers individuals to make informed decisions and interpret data effectively. Mastering this fundamental mathematical concept opens doors to a deeper understanding of the quantitative world around us. This article has provided a comprehensive guide to calculating percentages, exploring various methods and highlighting the practical relevance of this seemingly simple calculation in a wide array of contexts. By understanding the underlying principles and exploring different calculation approaches, you can develop a strong foundation for tackling more intricate percentage problems and effectively apply your knowledge in various real-world situations.
Latest Posts
Latest Posts
-
How Many Cups Are In A Pound Of Rice
Jul 10, 2025
-
How Many Pounds Is One Ton Equal
Jul 10, 2025
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 15 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.