120 Is What Percent Of 100
Kalali
Apr 11, 2025 · 5 min read
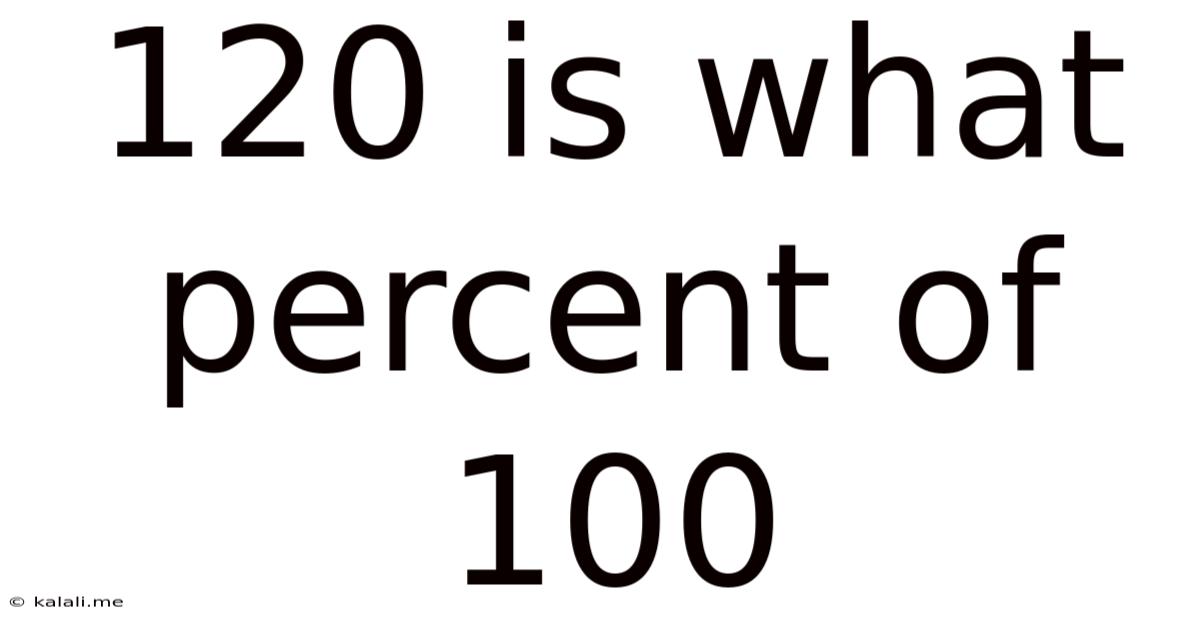
Table of Contents
120 is What Percent of 100? Understanding Percentage Calculations and Their Applications
This seemingly simple question, "120 is what percent of 100?", opens the door to a vast world of percentage calculations and their crucial role in various aspects of life. Understanding percentages is fundamental to interpreting data, making financial decisions, understanding statistics, and even excelling in various academic subjects. This article will not only answer the core question but also delve into the underlying principles, provide practical examples, and explore different methods for solving percentage problems.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percentage 120 represents of 100. This guide covers the basic formula, practical examples, and real-world applications of percentage calculations.
Answering the Core Question: 120 is What Percent of 100?
The straightforward answer is: 120 is 120% of 100. This might seem counterintuitive at first glance; how can a number be more than 100% of another number? The key here lies in understanding that percentages can represent values greater than the whole (100%). In this case, 120 exceeds 100 by 20, representing an additional 20% above the baseline of 100.
Understanding the Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
Let's break down this formula using our example:
- Part: This is the value we want to express as a percentage of the whole – in our case, 120.
- Whole: This is the base value to which we are comparing the part – in our case, 100.
- Percentage: This is the result we want to find, expressed as a percentage.
Applying the formula:
(120 / 100) x 100 = 120%
Therefore, 120 represents 120% of 100.
Different Methods for Calculating Percentages
While the standard formula is effective, there are alternative approaches to solving percentage problems, especially beneficial for mental calculations or situations where a calculator isn't readily available.
Method 1: Using Decimals
This method involves converting the percentage to a decimal and multiplying. To convert a percentage to a decimal, divide it by 100. For instance, 120% becomes 1.2 (120/100).
Then, multiply the decimal by the whole number:
1.2 x 100 = 120
This confirms that 120 is 120% of 100.
Method 2: Proportion Method
This method uses ratios to solve percentage problems. We can set up a proportion:
x/100 = 120/100
Solving for x:
x = (120/100) * 100 = 120
Again, this confirms that 120 is 120% of 100.
Method 3: Using the concept of "per cent"
The term "percent" literally translates to "per hundred". Therefore, to find what percent 120 is of 100, we ask: how many times does 100 fit into 120? The answer is 1.2 times. Multiplying 1.2 by 100 gives 120%, reinforcing our previous findings.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life. Understanding them is essential for navigating various situations effectively. Here are some examples:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, calculating a 15% discount on a $100 item involves finding 15% of $100, which is $15. The final price would be $85.
- Statistics and Data Analysis: Percentages are vital for representing data visually using charts and graphs (like pie charts and bar graphs) and for comparing different datasets. For example, analyzing the percentage increase or decrease in sales over time helps businesses understand their growth or decline.
- Academic Assessments: Grading systems often use percentages to represent student performance on exams and assignments. A score of 85% indicates the student answered 85 out of 100 questions correctly.
- Sales and Marketing: Analyzing conversion rates (percentage of website visitors who make a purchase), market share (percentage of a market held by a specific company), and customer satisfaction rates (percentage of satisfied customers) are crucial for business strategies.
- Everyday Life: Calculating tips in restaurants, understanding sales tax, and determining the percentage of ingredients in recipes all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
The example "120 is what percent of 100?" provides a fundamental understanding of percentage calculations. However, many real-world scenarios present more complex problems. Let's explore some variations:
- Finding the Whole when given the Part and Percentage: If a store offers a 20% discount on an item and the discount amount is $10, how much was the original price?
- We can set up the equation: 0.20 * x = $10. Solving for x gives x = $50, which is the original price.
- Finding the Part when given the Whole and Percentage: If a company wants to increase its sales by 10% next year, and current sales are $100,000, how much would their sales be next year?
- The increase would be 0.10 * $100,000 = $10,000. Their total sales next year would be $110,000.
- Percentage Change: Calculating the percentage increase or decrease between two values. For instance, if sales increased from $50,000 to $60,000, the percentage increase is ((60,000 - 50,000) / 50,000) x 100 = 20%.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's crucial for understanding long-term investments.
Mastering Percentage Calculations: Practice and Resources
The key to mastering percentage calculations is consistent practice. Solving various types of percentage problems, ranging from simple to complex, will build your understanding and proficiency. There are numerous online resources, including interactive calculators and practice exercises, that can aid in this process. These resources often offer different difficulty levels, allowing you to gradually improve your skills. Furthermore, understanding the underlying concepts of ratios and proportions will solidify your understanding of percentages.
Conclusion
The question "120 is what percent of 100?" serves as a gateway to understanding the broader world of percentage calculations. These calculations are vital for numerous aspects of life, from personal finance to professional endeavors. By mastering the basic formula and exploring different solution methods, you can confidently approach and solve a wide range of percentage problems, enhancing your analytical skills and decision-making capabilities. Remember to practice regularly and utilize available resources to strengthen your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Percent Is 9 Out Of 85
Apr 18, 2025
-
How Many Cups Is 16 9 Fluid Oz
Apr 18, 2025
-
2 To The Power Of 31
Apr 18, 2025
-
What Is 3 Out Of 20 As A Percentage
Apr 18, 2025
-
How Do You Know If A Table Is Linear
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 120 Is What Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.