13 Is What Percent Of 25
Kalali
Apr 12, 2025 · 4 min read
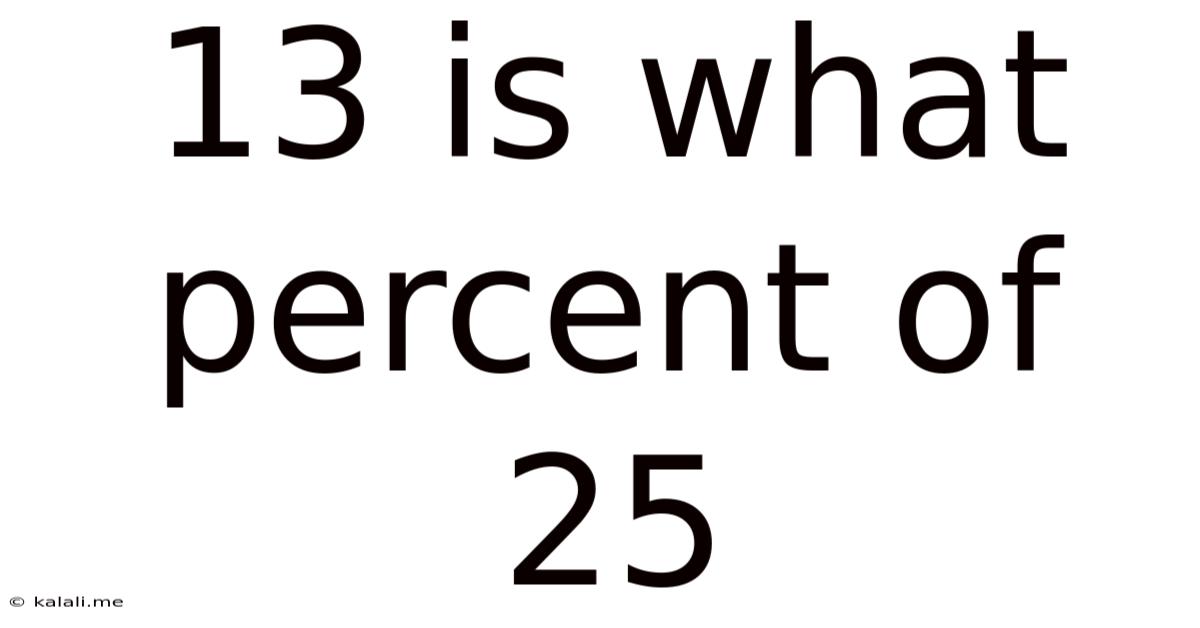
Table of Contents
13 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "13 is what percent of 25?", opens the door to a broader understanding of percentage calculations – a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This article will not only answer the question directly but also delve into the underlying principles, provide multiple methods for solving similar problems, and explore practical applications. Understanding percentages is crucial for interpreting data, making informed decisions, and navigating the numerical world around us.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "13 is what percent of 25?". This guide covers multiple methods, real-world applications, and practical tips for mastering percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages provide a standardized way to compare and understand proportions. They are widely used to express changes, rates, and proportions in various contexts.
Method 1: Using the Percentage Formula
The most common and direct method to solve "13 is what percent of 25?" involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 13 (the number we're considering as a portion of the whole)
- Whole: 25 (the total number)
Substituting these values into the formula:
(13 / 25) * 100% = 52%
Therefore, 13 is 52% of 25.
Method 2: Setting up a Proportion
Another effective approach uses proportions. A proportion expresses the equality of two ratios. We can set up a proportion as follows:
13/25 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
13 * 100 = 25 * x
1300 = 25x
x = 1300 / 25
x = 52
Therefore, x = 52%, confirming our previous result. This method emphasizes the relationship between fractions and percentages.
Method 3: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%.
First, divide the part by the whole:
13 / 25 = 0.52
Then, multiply the decimal by 100%:
0.52 * 100% = 52%
This approach highlights the connection between decimals and percentages. It's a particularly useful method when working with calculators or spreadsheets.
Practical Applications of Percentage Calculations
Percentage calculations are indispensable in a wide array of situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investments. Understanding percentage changes is crucial for tracking financial performance. For example, a 10% increase in sales revenue can be easily understood and compared against previous periods.
-
Statistics: Analyzing data, interpreting survey results, and understanding statistical significance. Percentages allow for the concise representation of large datasets. For instance, reporting that 60% of respondents favored a particular policy provides a clear and easily digestible summary.
-
Retail: Determining discounts, sales prices, and calculating markups. Retailers frequently use percentages to advertise special offers and attract customers.
-
Science: Expressing concentrations, error margins, and experimental results. In scientific contexts, accuracy and precision are paramount, and percentages provide a standardized means to express these aspects.
-
Everyday Life: Calculating tips, splitting bills, understanding nutritional information on food labels, and interpreting various statistics in news reports.
Advanced Percentage Calculations: Finding the Whole or the Part
While the initial problem focused on finding the percentage, percentage calculations can also involve finding the whole or the part given the percentage and another value.
Finding the Whole:
Let's say we know that 20% of a number is 10. To find the whole number, we can set up the following equation:
0.20 * x = 10
Solving for x:
x = 10 / 0.20
x = 50
Therefore, the whole number is 50.
Finding the Part:
Suppose we know that 60% of 80 is what number?
0.60 * 80 = x
x = 48
Therefore, 60% of 80 is 48.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to improve your skills is through consistent practice. Work through various problems, starting with simpler ones and gradually increasing the complexity.
-
Understand the Concepts: Don't just memorize formulas; strive to understand the underlying principles of percentages and their relationship to fractions and decimals.
-
Use Multiple Methods: Try solving problems using different approaches (formula, proportion, decimal conversion) to solidify your understanding and identify the most efficient method for each situation.
-
Check Your Work: Always double-check your calculations to avoid errors. Use a calculator if necessary, but make sure you understand the steps involved.
-
Real-World Application: Apply your knowledge to real-world scenarios to enhance your comprehension and retention. Look for opportunities to practice calculating percentages in your daily life.
Conclusion: Beyond the Calculation
The simple question, "13 is what percent of 25?" serves as a springboard to explore the versatile world of percentage calculations. By understanding the underlying principles and mastering various calculation methods, you equip yourself with a valuable skill applicable across numerous disciplines and everyday situations. Remember to practice consistently, understand the concepts, and apply your knowledge to real-world problems to solidify your understanding and improve your proficiency in this fundamental area of mathematics. The ability to confidently work with percentages empowers you to analyze data, make informed decisions, and navigate the numerical world with greater ease and understanding.
Latest Posts
Latest Posts
-
48 Inches Is How Many Cm
Apr 18, 2025
-
How Many Inches Is 22 5 Cm
Apr 18, 2025
-
52 Cm To Inches And Feet
Apr 18, 2025
-
What Is 74 Inches In Cm
Apr 18, 2025
-
31 Is What Percent Of 40
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 13 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.