15 Is What Percent Of 15
Kalali
Apr 14, 2025 · 5 min read
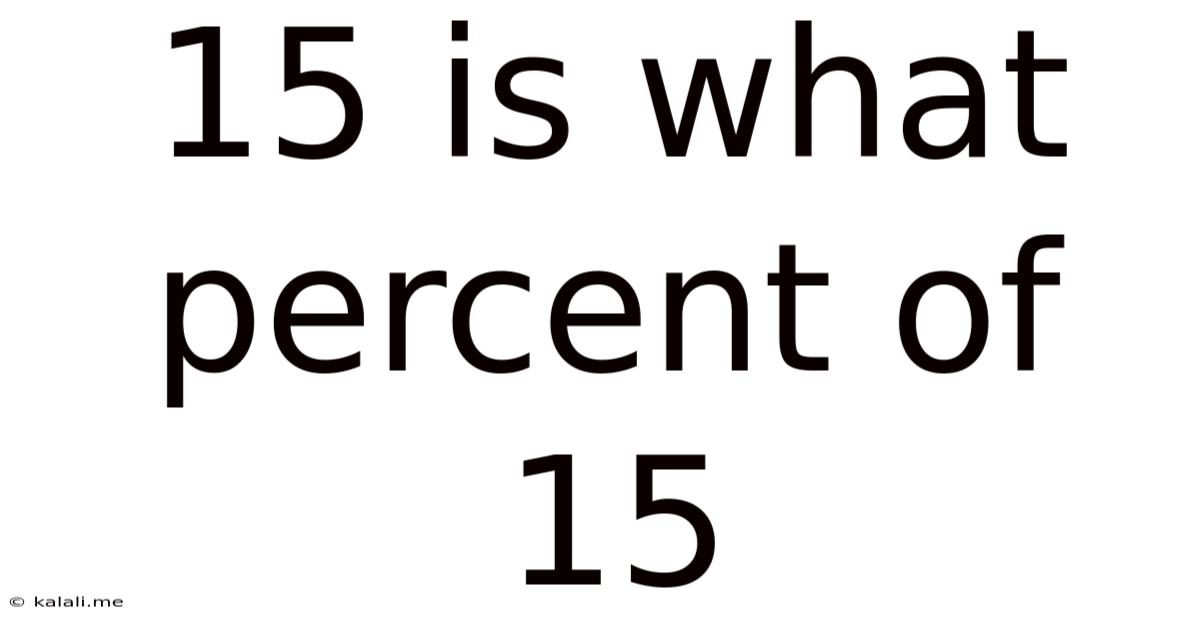
Table of Contents
15 is What Percent of 15? Unpacking the Concept of Percentage and its Applications
This seemingly simple question, "15 is what percent of 15?", opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life, finance, science, and more. This article will not only answer the question directly but also explore the underlying principles, demonstrate various calculation methods, and delve into practical examples to illustrate the significance of percentage calculations. Understanding percentages is crucial for interpreting data, making informed decisions, and navigating the numerical world around us. This in-depth guide will provide you with a comprehensive understanding, equipping you with the skills to confidently tackle similar percentage problems.
Understanding Percentages: A Foundation for Calculation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" – "per" meaning "for each" and "cent" meaning "hundred". Therefore, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. This fundamental understanding forms the basis for all percentage calculations.
Solving "15 is What Percent of 15?"
The direct answer to the question, "15 is what percent of 15?", is 100%. This is because 15 represents the whole amount (or 100%) in this specific case. Any number is 100% of itself.
Let's explore different methods to arrive at this answer, reinforcing the concept of percentage calculations:
Method 1: The Formula Approach
The standard formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
Part = 15 Whole = 15
Therefore:
(15 / 15) x 100% = 1 x 100% = 100%
This method clearly demonstrates how 15 is 100% of 15.
Method 2: Ratio and Proportion
We can also solve this using the concept of ratios and proportions. We can set up a proportion:
15/15 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
15 * 100 = 15 * x 1500 = 15x x = 1500 / 15 x = 100
This confirms that 15 is 100% of 15.
Method 3: Intuitive Understanding
The simplest approach, as mentioned earlier, involves understanding the concept directly. Since 15 is the entire amount being considered, it inherently represents the whole, which is always 100%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Finance: Calculating interest rates on loans and investments, understanding discounts and sales tax, analyzing financial statements, and tracking investment returns all rely heavily on percentage calculations. For example, if a bank offers a 5% interest rate on a savings account, understanding percentages allows you to calculate the interest earned on your deposits.
-
Retail: Determining discounts (e.g., a 20% off sale), calculating sales tax, and understanding profit margins are all based on percentage calculations. If a store offers a 25% discount on an item, you can use percentages to determine the final price.
-
Science: Expressing experimental results, analyzing data, and representing changes or growth rates often involve percentages. For instance, scientists may report that a certain drug increased effectiveness by 15%.
-
Education: Calculating grades, analyzing test scores, and representing progress are all based on percentage calculations. A student's final grade is often expressed as a percentage of the total possible points.
-
Everyday Life: Calculating tips in restaurants, understanding nutrition labels (e.g., percentage of daily value for nutrients), and interpreting statistics in news reports are common examples of the everyday use of percentages.
Beyond the Basics: More Complex Percentage Problems
While the question "15 is what percent of 15?" provides a foundational understanding, let's explore more complex scenarios to broaden your skills:
-
Finding the Percentage Increase or Decrease: Suppose the price of an item increased from $10 to $15. To find the percentage increase:
- Calculate the difference: $15 - $10 = $5
- Divide the difference by the original price: $5 / $10 = 0.5
- Multiply by 100% to express as a percentage: 0.5 x 100% = 50%
Therefore, the price increased by 50%.
-
Finding a Percentage of a Number: What is 20% of 50?
- Convert the percentage to a decimal: 20% = 0.20
- Multiply the decimal by the number: 0.20 x 50 = 10
Therefore, 20% of 50 is 10.
-
Finding the Original Amount: If 15% of a number is 3, what is the original number?
- Set up an equation: 0.15x = 3
- Solve for x: x = 3 / 0.15 = 20
Therefore, the original number is 20.
Tips and Tricks for Mastering Percentage Calculations
-
Memorize common percentage equivalents: Knowing that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75% can significantly speed up calculations.
-
Use a calculator: For more complex calculations, a calculator can save time and ensure accuracy.
-
Practice regularly: The more you practice percentage calculations, the more comfortable and proficient you will become.
-
Break down complex problems: Divide complex problems into smaller, more manageable steps.
-
Check your work: Always double-check your answers to ensure accuracy.
Conclusion:
While "15 is what percent of 15?" may appear simple at first glance, it serves as a vital stepping stone to understanding the broader concept of percentages and their crucial role in various aspects of life. Mastering percentage calculations empowers you to analyze data effectively, make informed decisions, and navigate the numerical world with confidence. By understanding the fundamental principles and applying the methods outlined in this article, you can confidently tackle any percentage problem you encounter. Remember to practice regularly, and you will soon find yourself adept at working with percentages in any context.
Latest Posts
Latest Posts
-
How Many Cups Are In A Pound Of Rice
Jul 10, 2025
-
How Many Pounds Is One Ton Equal
Jul 10, 2025
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.