15 Is What Percent Of 150
Kalali
Apr 13, 2025 · 5 min read
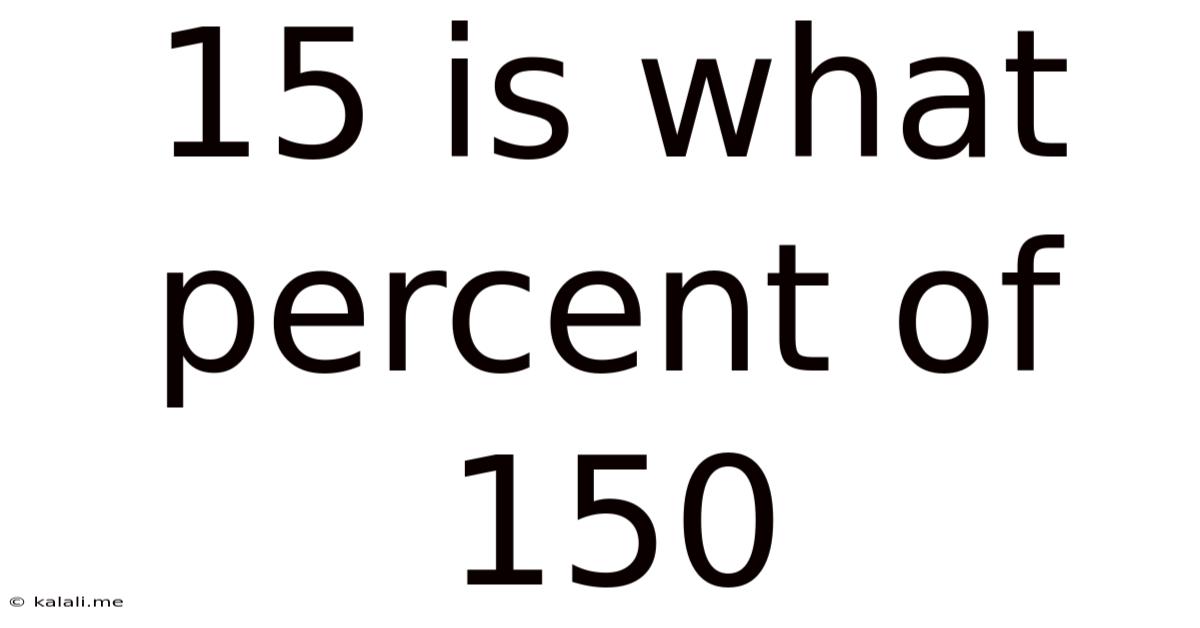
Table of Contents
15 is What Percent of 150? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve deep into the question, "15 is what percent of 150?", providing not only the answer but also a comprehensive explanation of the underlying concepts and methods for solving percentage problems. We'll cover different approaches, helpful tips, and real-world applications to solidify your understanding. This guide will serve as a valuable resource for students, professionals, and anyone seeking to improve their proficiency in percentage calculations.
Meta Description: Learn how to calculate percentages effectively! This comprehensive guide explains how to determine what percent 15 is of 150, covering various methods, real-world examples, and helpful tips for mastering percentage calculations.
Understanding Percentages: The Basics
Before diving into the specific problem, let's establish a solid foundation in percentage calculations. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of one hundred." For instance, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5.
The fundamental formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
Where:
- Part: The specific amount you're interested in expressing as a percentage.
- Whole: The total amount or the base value.
- Percentage: The result expressed as a percentage.
Method 1: Direct Calculation Using the Formula
Let's apply this formula to our question: "15 is what percent of 150?"
In this case:
- Part = 15
- Whole = 150
Substituting these values into the formula:
(15 / 150) x 100 = Percentage
Simplifying the fraction:
(1/10) x 100 = 10
Therefore, 15 is 10% of 150.
Method 2: Using Proportions
Another effective way to solve percentage problems is by setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
15/150 = x/100
Where:
- 15 represents the part.
- 150 represents the whole.
- x represents the unknown percentage.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
15 * 100 = 150 * x
1500 = 150x
Now, divide both sides by 150:
x = 1500 / 150
x = 10
Therefore, again, 15 is 10% of 150.
Method 3: Using Decimal Conversion
This method involves converting the fraction (Part/Whole) into a decimal and then multiplying by 100 to express it as a percentage.
- Convert the fraction: 15/150 = 0.1
- Multiply by 100: 0.1 x 100 = 10%
This method is particularly useful when dealing with calculators and reinforces the understanding of the relationship between decimals and percentages.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-life scenarios. Here are a few examples:
- Sales and Discounts: Calculating the discount amount on sale items. For example, a 20% discount on a $100 item means a $20 discount ($100 x 0.20 = $20).
- Taxes: Determining the amount of tax payable on purchases or income.
- Financial Analysis: Analyzing financial statements, calculating profit margins, and understanding growth rates.
- Statistics and Data Analysis: Expressing data as percentages to facilitate comparisons and draw meaningful conclusions.
- Grade Calculations: Calculating grades based on scores obtained in tests and assignments.
- Tipping: Calculating appropriate tips in restaurants or for services rendered.
- Interest Rates: Calculating simple and compound interest on loans or investments.
- Surveys and Polls: Interpreting survey results and representing data in percentage form.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations. Try solving different types of percentage problems to strengthen your understanding.
- Understand the Formula: Thoroughly grasp the basic formula and its variations.
- Use a Calculator: Calculators can simplify calculations, particularly when dealing with complex numbers.
- Break Down Complex Problems: If faced with a complex problem, break it down into smaller, manageable steps.
- Check Your Work: Always verify your calculations to ensure accuracy.
Beyond the Basics: More Complex Percentage Problems
While the problem "15 is what percent of 150?" is relatively straightforward, percentage calculations can become more complex. Here are some examples of more advanced scenarios:
- Finding the Whole: Knowing the percentage and the part, calculate the whole. For instance, if 25% of a number is 50, what is the number?
- Finding the Part: Knowing the percentage and the whole, calculate the part. For example, what is 15% of 200?
- Percentage Increase/Decrease: Calculating the percentage change between two values. For instance, if a value increases from 100 to 120, what is the percentage increase?
- Compound Interest: Calculating interest that accrues not only on the principal amount but also on accumulated interest.
- Percentage Points vs. Percentages: Understanding the difference between percentage points and percentages is crucial for accurate interpretation of data.
Conclusion: Mastering the Art of Percentages
Understanding percentages is an essential skill with broad applications. This article comprehensively addressed the question "15 is what percent of 150?" and provided various methods for solving such problems. By understanding the fundamental formula, utilizing different approaches, and practicing regularly, you can develop proficiency in percentage calculations and apply this knowledge effectively in diverse real-world scenarios. Remember to always check your work and break down complex problems into smaller, manageable steps. With practice and consistent effort, you'll master the art of percentages and confidently tackle any percentage-related challenge.
Latest Posts
Latest Posts
-
A Net Force Of One Newton Will
Apr 14, 2025
-
A Hydraulic Motor Converts Fluid Pressure To
Apr 14, 2025
-
Is Oil And Water A Heterogeneous Mixture
Apr 14, 2025
-
How Many Seconds Are In 30 Mins
Apr 14, 2025
-
15 Out Of 19 As A Percentage
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.