150 Is What Percent Of 75
Kalali
Apr 25, 2025 · 5 min read
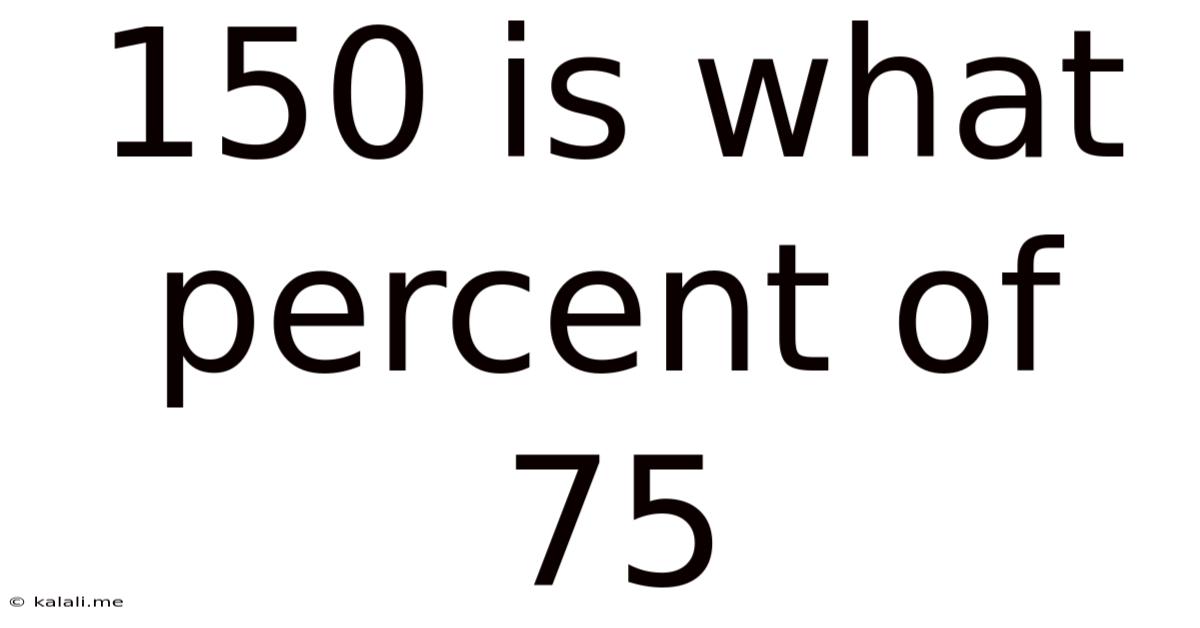
Table of Contents
150 is What Percent of 75? Understanding Percentage Calculations and Their Applications
This seemingly simple question, "150 is what percent of 75?", opens the door to a broader understanding of percentage calculations, their practical applications, and how to approach similar problems with confidence. At first glance, it might seem counterintuitive – how can a smaller number be a percentage of a larger number? The answer lies in the concept of percentages and their representation as proportions. This article will not only answer the initial question but also delve into the methodology, explore real-world examples, and provide you with the tools to tackle any percentage problem.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to determine what percentage 150 represents of 75, covering the methodology, real-world applications, and providing you with the skills to solve similar percentage problems.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). We use percentages to represent parts of a whole in a standardized way, making comparisons and calculations easier. For instance, 50% means 50 out of 100, or one-half.
Understanding this fundamental principle is key to solving percentage problems. It allows us to translate word problems into mathematical equations and find solutions efficiently.
Solving "150 is What Percent of 75?"
The question "150 is what percent of 75?" can be expressed as a mathematical equation:
x% * 75 = 150
where 'x' represents the unknown percentage. To solve for 'x', we need to isolate it on one side of the equation.
-
Divide both sides by 75:
x% = 150 / 75 -
Simplify:
x% = 2 -
Convert to percentage:
Since x represents a percentage, we need to multiply it by 100 to express it in percentage form.
x = 2 * 100 = 200%
Therefore, 150 is 200% of 75. This result might seem surprising at first, but it highlights the flexibility of percentages in representing values greater than the whole.
Why the Result is Greater Than 100%
The result of 200% is perfectly valid and signifies that 150 is twice the value of 75. Percentages aren't limited to values between 0% and 100%; they can exceed 100% to represent values larger than the reference value. Think of it like this: if you have 75 apples and then obtain another 75 apples, you'll have 150 apples, which is 200% of your original amount.
Different Ways to Calculate Percentages
While the method above is straightforward, there are alternative approaches to calculate percentages, particularly useful for different types of problems.
Method 1: Using a Proportion
Set up a proportion:
x/100 = 150/75
Cross-multiply and solve for x:
75x = 15000
x = 15000/75
x = 200
Therefore, x = 200%, which is the same result as before.
Method 2: Using Decimal Conversion
Convert the percentage to a decimal by dividing by 100. Let's say you want to find what percentage 150 is of 75, this equation is used:
x = (150 / 75)
x = 2
To express it as a percentage, multiply the result by 100. This is why our answer is 200%.
These alternative methods offer flexibility depending on the complexity and context of the problem.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life, across various fields:
-
Finance: Calculating interest rates, loan repayments, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, a 10% discount on a $100 item means a reduction of $10.
-
Business: Analyzing market share, tracking sales growth, assessing customer satisfaction, and projecting future performance often involve percentages.
-
Science: Expressing experimental results, calculating statistical probabilities, and representing data in graphs and charts commonly use percentages.
-
Education: Grading systems, test scores, and performance evaluations all utilize percentages to measure student achievement.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, and interpreting survey results require an understanding of percentages.
Advanced Percentage Problems
While the initial problem was relatively straightforward, let's explore more complex scenarios that require a deeper understanding of percentage calculations:
Scenario 1: Percentage Increase/Decrease
Suppose the price of an item increased from $75 to $150. To calculate the percentage increase, we can use the following formula:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
Percentage Increase = [(150 - 75) / 75] * 100 = 100%
The price increased by 100%.
Scenario 2: Finding the Original Value
If an item is currently priced at $150 after a 50% increase, what was the original price? This requires working backward:
Let 'x' be the original price.
x + 0.5x = 150
1.5x = 150
x = 150 / 1.5 = $100
The original price was $100.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The more you practice solving percentage problems, the more comfortable you'll become with the concepts and techniques.
-
Understand the Fundamentals: A strong grasp of fractions, decimals, and ratios is essential for mastering percentage calculations.
-
Use Different Methods: Experiment with different approaches to solving problems to find the method that works best for you.
-
Break Down Complex Problems: Divide complex percentage problems into smaller, more manageable steps.
-
Check Your Work: Always double-check your calculations to ensure accuracy. You can use a calculator to verify your results.
Conclusion
The seemingly simple question, "150 is what percent of 75?", serves as a gateway to a world of percentage calculations and their broad applications. Understanding the underlying principles, exploring various solution methods, and practicing regularly will equip you to confidently tackle any percentage problem, regardless of its complexity. From financial planning to everyday decision-making, a strong grasp of percentages is an invaluable skill. This article has provided a comprehensive overview, equipping you with the knowledge and tools to navigate the world of percentages with ease and accuracy. Remember that mastering percentages is a journey of consistent practice and understanding. Keep practicing, and you'll soon find yourself effortlessly solving even the most challenging percentage problems.
Latest Posts
Latest Posts
-
108 Cm To Inches And Feet
Apr 26, 2025
-
What Is The Lifespan Of A Crocodile
Apr 26, 2025
-
2000 Milligrams Is Equal To How Many Grams
Apr 26, 2025
-
Five Ounces Equals How Many Cups
Apr 26, 2025
-
What Percent Is 22 Of 40
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about 150 Is What Percent Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.