16 Is What Percent Of 40
Kalali
Apr 15, 2025 · 5 min read
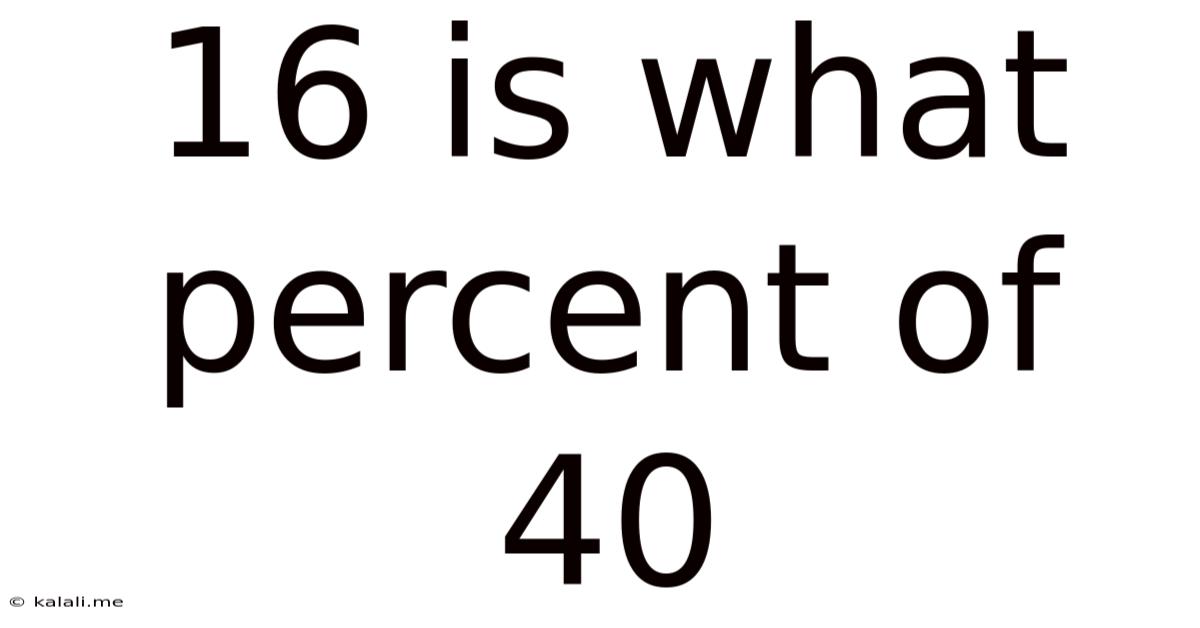
Table of Contents
16 is What Percent of 40? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "16 is what percent of 40?", opens the door to a fascinating world of percentage calculations and their widespread applications in everyday life, from finance and shopping to science and statistics. This article will not only answer the question directly but also explore the underlying mathematical concepts, provide different methods for solving similar problems, and demonstrate the practical relevance of percentages across various fields.
Meta Description: Learn how to calculate percentages with a comprehensive guide that solves "16 is what percent of 40?" and explores diverse applications of percentage calculations in everyday life, from finance to science. Master percentage problems and improve your mathematical skills.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (from the Latin per centum). Therefore, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental concept is key to tackling percentage problems effectively.
Method 1: The Proportion Method
This is arguably the most straightforward and intuitive method for solving percentage problems. We set up a proportion, equating two ratios:
- Ratio 1: The given part (16) to the whole (40)
- Ratio 2: The unknown percentage (x) to 100
This translates into the following equation:
16/40 = x/100
To solve for x, we cross-multiply:
16 * 100 = 40 * x
1600 = 40x
Now, divide both sides by 40:
x = 1600 / 40
x = 40
Therefore, 16 is 40% of 40.
Method 2: The Decimal Method
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
First, express the given part as a fraction of the whole:
16/40
Then, simplify the fraction (if possible):
16/40 = 2/5
Next, convert the fraction to a decimal by dividing the numerator by the denominator:
2 ÷ 5 = 0.4
Finally, multiply the decimal by 100 to obtain the percentage:
0.4 * 100 = 40%
So, again, we find that 16 is 40% of 40.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply divide the part (16) by the whole (40) and then multiply by 100.
16 ÷ 40 * 100 = 40%
Applications of Percentage Calculations in Real Life
The ability to calculate percentages is a crucial skill with applications in various aspects of daily life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage change is vital for tracking the growth or decline of investments. For example, calculating compound interest involves repeated percentage calculations.
-
Shopping: Discounts are often expressed as percentages. Calculating the final price after a discount involves subtracting the percentage discount from the original price. Sales tax is also calculated as a percentage of the purchase price.
-
Science: Percentages are used extensively in scientific fields like chemistry (concentration of solutions), biology (population growth rates), and statistics (probability and data analysis). Understanding percentage error is critical for evaluating the accuracy of scientific measurements.
-
Statistics: Percentages are used to represent proportions within datasets, facilitating comparisons and drawing conclusions. For instance, analyzing survey results often involves calculating percentages to represent responses to particular questions.
-
Everyday Life: Understanding percentages helps in making informed decisions in various situations. For example, comparing the fuel efficiency of cars, analyzing nutritional information on food labels, or calculating tips at restaurants.
Solving More Complex Percentage Problems
While the example "16 is what percent of 40?" is relatively simple, understanding the underlying principles allows you to tackle more complex percentage problems:
Example 1: Finding the whole when given a part and a percentage:
If 25% of a number is 15, what is the number?
Let the number be x. We can set up the equation:
0.25x = 15
x = 15 / 0.25
x = 60
Therefore, the number is 60.
Example 2: Finding the percentage increase or decrease:
A product's price increased from $50 to $60. What is the percentage increase?
Percentage increase = [(New Value - Old Value) / Old Value] * 100
Percentage increase = [(60 - 50) / 50] * 100
Percentage increase = (10 / 50) * 100
Percentage increase = 20%
Example 3: Calculating Percentage Change with Negative Values:
A company's profit decreased from $100,000 to $80,000. What is the percentage decrease?
Percentage decrease = [(Old Value - New Value) / Old Value] * 100
Percentage decrease = [(100,000 - 80,000) / 100,000] * 100
Percentage decrease = (20,000 / 100,000) * 100
Percentage decrease = 20%
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Start with simple problems and gradually move to more complex ones.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages. This will help you solve problems more efficiently and adapt to various scenarios.
-
Use Different Methods: Experiment with different methods – the proportion method, the decimal method, and using a calculator – to find the approach that suits you best.
-
Check Your Answers: Always check your answers to ensure accuracy. You can do this by working backward from your answer or using a different method to verify your result.
-
Utilize Online Resources: Numerous online resources, including practice problems and tutorials, can help you improve your understanding and skills in calculating percentages.
By understanding the fundamental principles and applying the different methods described above, you can confidently tackle any percentage problem, from simple calculations like "16 is what percent of 40?" to more complex scenarios encountered in various real-world applications. Mastering percentage calculations is a valuable skill that will enhance your problem-solving abilities and help you make informed decisions in numerous aspects of your life.
Latest Posts
Latest Posts
-
A Trapezoid Always Has Two Congruent Sides
Apr 16, 2025
-
How Many Seconds In 8 Minutes
Apr 16, 2025
-
15 Is 60 Of What Number
Apr 16, 2025
-
How Many Glasses Of Water In 32 Oz
Apr 16, 2025
-
If A Ferrari With An Initial Velocity Of 10m S
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.