16 To The Power Of 2
Kalali
Mar 28, 2025 · 6 min read
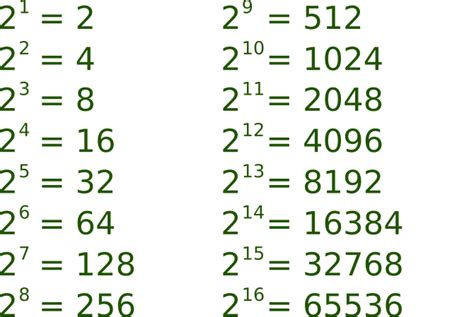
Table of Contents
16 to the Power of 2: Exploring the Math, Applications, and Beyond
16 to the power of 2, often written as 16², is a seemingly simple mathematical expression. However, delving into its calculation, its applications across various fields, and its connections to broader mathematical concepts reveals a fascinating journey into the world of numbers. This comprehensive guide explores the multifaceted nature of 16², its significance, and its implications beyond simple arithmetic.
Calculating 16²: The Basics
The expression 16² represents 16 multiplied by itself: 16 x 16. Performing this simple multiplication gives us the answer: 256. This fundamental calculation forms the bedrock for understanding more complex applications. Understanding this basic calculation is crucial for building a foundation in more advanced mathematical concepts. It's the first step towards grasping exponential growth, quadratic equations, and other related areas.
Beyond the Calculation: Understanding Exponents
The concept of exponents, represented by the superscript number (the "2" in 16²), signifies repeated multiplication. It's a concise way of expressing a number multiplied by itself a certain number of times. For example:
- 2³ = 2 x 2 x 2 = 8 (2 raised to the power of 3)
- 5² = 5 x 5 = 25 (5 raised to the power of 2)
- 10¹ = 10 (10 raised to the power of 1, which is simply 10 itself)
- x⁰ = 1 (any number raised to the power of 0 equals 1, excluding 0⁰ which is undefined)
Understanding exponents is crucial in various fields, from computer science to finance, as it's essential for modeling exponential growth and decay. Mastering this foundational concept unlocks a deeper understanding of more complex mathematical models. The simple calculation of 16² is a stepping stone to mastering more intricate exponential functions.
Applications of 16² in Different Fields
The seemingly simple result of 16² (256) appears surprisingly frequently in various applications, showcasing its importance across diverse disciplines:
1. Computer Science and Data Storage
The number 256 holds significant importance in computer science. It’s directly related to the number of values that can be represented by an 8-bit byte (2⁸ = 256). This is because each bit can represent either a 0 or a 1, leading to 256 possible combinations. This impacts how computers store and process data, influencing everything from image resolution to character encoding. Understanding this connection between 16², 2⁸, and 256 is vital for computer programmers and anyone working with digital data.
2. Image Resolution and Pixel Dimensions
In digital imaging, 256 often appears as a common factor in image resolution. For example, an image with a resolution of 256 x 256 pixels utilizes 256 pixels in both its width and height dimensions. This relates directly back to the 8-bit byte and its ability to represent 256 distinct values, influencing the color depth and overall quality of the image.
3. Networking and IP Addresses (Historically)
While less relevant in current IPv6 addressing, historically, 256 played a role in the structure of IPv4 IP addresses. Each octet (group of 8 bits) in an IPv4 address could represent a number between 0 and 255, a direct consequence of the 256 possible values represented by 8 bits.
4. Mathematics and Geometry
In geometry, 256 might appear in various calculations, particularly those involving squares, cubes, and higher-dimensional objects. It can be a factor in area calculations, volume calculations, and other geometric computations. Its prevalence in computational geometry further highlights its numerical significance.
5. Finance and Compound Interest
While not directly involved in basic interest calculations, 256 could indirectly impact calculations involving exponential growth, such as compound interest. As the number of compounding periods increases, the growth becomes exponential, often leading to results containing numbers like 256 or its multiples, depending on the initial principal and interest rate.
Exploring Related Concepts: Powers of 2
16² is a member of the family of powers of 2. The powers of 2 (2 raised to various exponents) are: 2¹, 2², 2³, 2⁴, and so on. This sequence (2, 4, 8, 16, 32, 64, 128, 256, 512, and so on) plays a crucial role in various areas of mathematics and computer science, due to its binary nature, which is perfectly suited to digital systems. The fact that 16 is itself a power of 2 (2⁴) makes 16² (256) a significant member of this important sequence.
Expanding on the Concept: Larger Powers
Understanding 16² lays the groundwork for understanding larger powers. For example, 16³ (16 to the power of 3) is 16 x 16 x 16 = 4096. Similarly, calculating higher powers helps build an intuition for exponential growth and how numbers can rapidly increase. As exponents increase, the resulting numbers grow exponentially larger, highlighting the dramatic impact of exponents on numerical values.
Practical Applications: Using 16² in Calculations
Understanding how 16² is used practically is crucial for applying the knowledge. Let's consider a couple of examples:
-
Area Calculation: If you have a square with sides of 16 units (meters, centimeters, inches, etc.), the area of the square is 16² = 256 square units. This is a direct and fundamental application of this mathematical concept.
-
Data Storage Estimation: If you need to store data that requires 256 unique values (e.g., representing colors in an image), you'll need a system that can accommodate 8 bits (or one byte) per value, directly stemming from the relationship between 256 and 8-bit storage.
Connecting 16² to Broader Mathematical Principles
16² isn't just an isolated calculation; it connects to various broader mathematical principles:
-
Perfect Squares: 256 is a perfect square, meaning it's the square of an integer (16). Understanding perfect squares is crucial in various areas of mathematics, including algebra and geometry.
-
Binary Numbers: The close relationship between 256 and the binary number system highlights the importance of powers of 2 in computing and digital systems. 256 is 100000000 in binary, a direct representation that highlights its significance in computer science.
-
Exponential Functions: 16² provides a simple but effective illustration of exponential functions, showcasing how even a small exponent can produce a significant result. This underlies the concept of exponential growth and decay, seen in various real-world phenomena.
Conclusion: The Significance of 16²
While 16² might seem like a simple arithmetic problem, its significance extends far beyond the basic calculation. The number 256, the result of 16², appears frequently in computer science, data storage, image resolution, and even indirectly in finance and geometry. Understanding its calculation, its application in various fields, and its connection to broader mathematical principles provides a deeper appreciation of its importance in both theoretical and practical contexts. This journey through 16² highlights the power of seemingly simple mathematical concepts and their surprising impact on various aspects of our lives. The depth of this seemingly basic calculation underscores the interconnectedness and power of mathematics in understanding and shaping our world. Further exploration of exponents, powers of two, and binary systems will only enhance your understanding of the significance of 16² and its far-reaching implications.
Latest Posts
Latest Posts
-
What Is The Percentage Of 7 Out Of 8
Mar 31, 2025
-
How Many Inches Is 30 Ft
Mar 31, 2025
-
What Is The Boiling Point Of Saltwater
Mar 31, 2025
-
What Are The 2 Parts Of A Solution
Mar 31, 2025
-
What Are The Chemical Equations Of Photosynthesis And Cellular Respiration
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 16 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
