160 Is What Percent Of 40
Kalali
Apr 09, 2025 · 4 min read
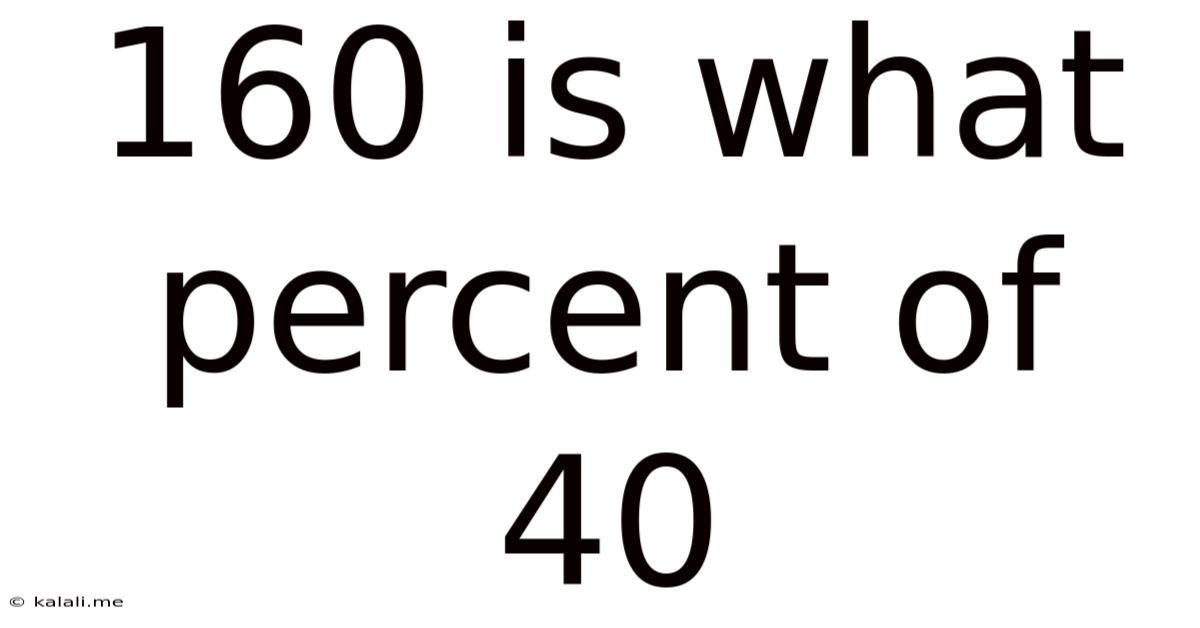
Table of Contents
160 is What Percent of 40? Understanding Percentages and Their Applications
This seemingly simple question – "160 is what percent of 40?" – opens the door to a vast world of mathematical concepts and practical applications. It's more than just a basic percentage problem; it's a gateway to understanding how percentages are used in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will not only answer the question directly but also explore the underlying principles, provide multiple methods for solving similar problems, and illustrate real-world applications of percentage calculations.
Meta Description: Learn how to calculate percentages with a step-by-step guide solving "160 is what percent of 40?". Discover different calculation methods and explore real-world applications of percentage calculations in finance, statistics, and more.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of one hundred." Understanding this fundamental concept is key to solving percentage problems. For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Solving "160 is What Percent of 40?" - Method 1: The Proportion Method
The most straightforward method to solve this problem involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
- Part/Whole = Percentage/100
In our case:
- Part: 160
- Whole: 40
- Percentage: 'x' (this is what we need to find)
Therefore, our proportion becomes:
160/40 = x/100
To solve for 'x', we cross-multiply:
160 * 100 = 40 * x
16000 = 40x
Now, divide both sides by 40:
x = 16000 / 40
x = 400
Therefore, 160 is 400% of 40.
Solving "160 is What Percent of 40?" - Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then solving the equation.
First, we set up the equation:
160 = x * 40
where 'x' represents the percentage expressed as a decimal.
To solve for 'x', we divide both sides by 40:
x = 160 / 40
x = 4
Since 'x' is a decimal representing the percentage, we convert it back to a percentage by multiplying by 100:
x = 4 * 100
x = 400%
Therefore, again, we find that 160 is 400% of 40.
Why is the Percentage Greater Than 100%?
The result of 400% might seem counterintuitive at first. Percentages greater than 100% simply indicate that the "part" is larger than the "whole." In this case, 160 is more than four times greater than 40. This often happens in contexts involving growth, increase, or comparisons where the final value exceeds the initial value.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous real-world scenarios:
- Finance: Calculating interest rates, loan repayments, profit margins, investment returns, and tax percentages.
- Sales and Marketing: Determining discounts, markups, sales growth, and market share.
- Statistics and Data Analysis: Representing proportions, calculating percentages of populations, and analyzing data trends.
- Everyday Life: Calculating tips, understanding nutrition labels (percentage of daily values), and interpreting survey results.
More Examples and Practice Problems
Let's work through a few more examples to solidify your understanding:
Example 1: What percent of 25 is 5?
Using the proportion method:
5/25 = x/100
500 = 25x
x = 20
Therefore, 5 is 20% of 25.
Example 2: 30 is what percent of 150?
Using the decimal method:
30 = x * 150
x = 30/150
x = 0.2
x = 0.2 * 100 = 20%
Therefore, 30 is 20% of 150.
Example 3: A shirt originally priced at $50 is on sale for $35. What is the percentage discount?
First, calculate the amount of the discount: $50 - $35 = $15
Then, calculate the percentage discount: ($15/$50) * 100 = 30%
Advanced Percentage Concepts: Percentage Change and Percentage Points
Beyond basic percentage calculations, it's important to understand more complex concepts:
-
Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. For example, if a stock price increases from $10 to $12, the percentage change is [(12-10)/10] * 100 = 20%.
-
Percentage Points: This represents the absolute difference between two percentages. For instance, if interest rates increase from 2% to 5%, the increase is 3 percentage points, not 150% (which would be the percentage change).
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately and efficiently is a valuable skill in various aspects of life. While the question "160 is what percent of 40?" might seem simple on the surface, it provides a solid foundation for understanding percentages and their diverse applications. By mastering the different calculation methods and understanding related concepts, you can confidently tackle percentage problems and leverage this knowledge for practical purposes. Remember to practice regularly to further enhance your skills and problem-solving capabilities. The more you work with percentages, the more intuitive they will become.
Latest Posts
Latest Posts
-
How Much Is 2000 Ml In Oz
Apr 17, 2025
-
How Many Mm Are In 6 Cm
Apr 17, 2025
-
What Percent Is 60 Of 150
Apr 17, 2025
-
What Is 89 Cm In Inches
Apr 17, 2025
-
How Many Hours And Minutes Is 225 Minutes
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 160 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.