17 Out Of 31 As A Percentage
Kalali
Apr 06, 2025 · 4 min read
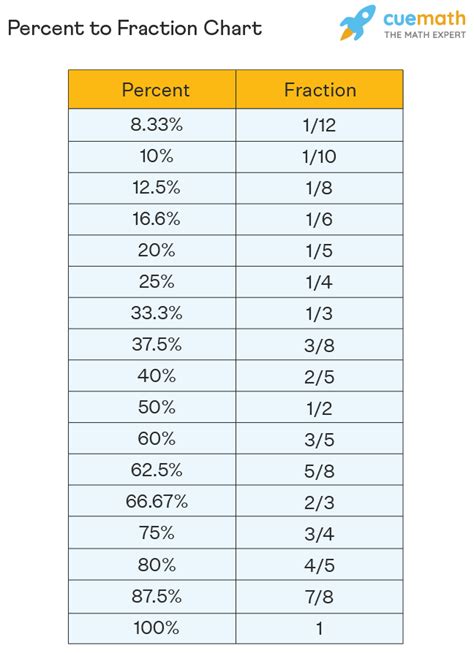
Table of Contents
17 out of 31 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in various aspects of life, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and excelling in academic and professional settings. This article will delve deep into calculating "17 out of 31 as a percentage," providing not only the answer but also a comprehensive explanation of the process and its applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or 0.5 as a decimal. Percentages are versatile and widely used because they allow for easy comparison of different proportions.
Calculating 17 out of 31 as a Percentage
To calculate 17 out of 31 as a percentage, we follow these steps:
1. Express the Fraction:
First, we represent "17 out of 31" as a fraction: 17/31.
2. Convert the Fraction to a Decimal:
To convert the fraction to a decimal, we divide the numerator (17) by the denominator (31):
17 ÷ 31 ≈ 0.548387
3. Convert the Decimal to a Percentage:
To convert the decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%):
0.548387 × 100 ≈ 54.84%
Therefore, 17 out of 31 is approximately 54.84%.
Rounding and Precision
The result, 54.84%, is a rounded figure. The actual decimal value is a non-terminating decimal, meaning it continues infinitely. The level of rounding depends on the context. For most purposes, two decimal places (54.84%) offer sufficient accuracy. However, in situations requiring higher precision, more decimal places may be necessary.
Practical Applications of Percentage Calculations
The ability to calculate percentages has wide-ranging applications across numerous fields:
1. Academic Performance
Calculating percentages is fundamental in assessing academic performance. For instance, if a student answers 17 questions correctly out of a total of 31 questions on a test, their score would be approximately 54.84%.
2. Financial Calculations
Percentages are ubiquitous in finance. Interest rates, discounts, tax calculations, profit margins, and investment returns are all expressed as percentages. Understanding percentage calculations is essential for managing personal finances and making informed investment decisions.
3. Statistical Analysis
Percentages are crucial in statistical analysis for representing proportions and making comparisons within datasets. For example, in market research, percentages are used to represent the proportion of consumers who prefer a particular product or service.
4. Business and Economics
Percentages are essential for analyzing business performance. Profit margins, sales growth rates, market share, and unemployment rates are all expressed as percentages.
5. Science and Engineering
Percentages are used to represent quantities and proportions in scientific and engineering calculations. For instance, in chemistry, percentages are used to represent the concentration of a solution.
6. Everyday Life
From calculating tips in restaurants to understanding sales discounts, percentages are frequently encountered in daily life. Mastering percentage calculations simplifies these everyday tasks.
Advanced Percentage Calculations: Beyond the Basics
While calculating 17 out of 31 as a percentage is straightforward, let's explore more complex percentage-related problems:
1. Finding the Percentage Increase or Decrease
Imagine a product's price increases from $31 to $48. To calculate the percentage increase, follow these steps:
- Find the difference: $48 - $31 = $17
- Divide the difference by the original price: $17 / $31 ≈ 0.5484
- Multiply by 100 to get the percentage: 0.5484 × 100 ≈ 54.84%
Therefore, the price increased by approximately 54.84%. The same principle applies to calculating percentage decreases.
2. Finding the Original Value
Suppose a product is on sale at a 45% discount, and its current price is $17. To find the original price, we use the following method:
- Let 'x' be the original price. The discounted price is 55% (100% - 45%) of the original price.
- Set up an equation: 0.55x = $17
- Solve for x: x = $17 / 0.55 ≈ $30.91
Therefore, the original price was approximately $30.91.
3. Working with Multiple Percentages
Sometimes you need to calculate multiple percentages sequentially. For example, suppose a product is first discounted by 20%, and then an additional 10% is taken off the discounted price. The final price will not be simply a 30% discount. You must calculate each discount step by step.
Using Calculators and Spreadsheets
For more complex percentage calculations, or for dealing with large datasets, using a calculator or spreadsheet software like Microsoft Excel or Google Sheets is highly recommended. These tools offer built-in functions for calculating percentages, making the process much faster and less prone to errors.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is an invaluable skill that extends far beyond the classroom. From navigating daily financial transactions to analyzing complex data, the ability to convert fractions and decimals into percentages empowers you to make informed decisions and effectively communicate numerical information. This article provided a detailed explanation of calculating "17 out of 31 as a percentage," along with various applications and advanced techniques, equipping you with the knowledge to tackle a broad range of percentage-related problems. Remember, consistent practice is key to mastering this essential skill. By incorporating these techniques and using available tools, you can confidently approach and solve any percentage calculation you encounter.
Latest Posts
Latest Posts
-
5 Out Of 20 As A Percentage
Apr 07, 2025
-
What Percentage Of 30 Is 12
Apr 07, 2025
-
A Life Cycle Of A Bean Plant
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 31 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.