18 Out Of 21 As A Percentage
Kalali
Apr 08, 2025 · 5 min read
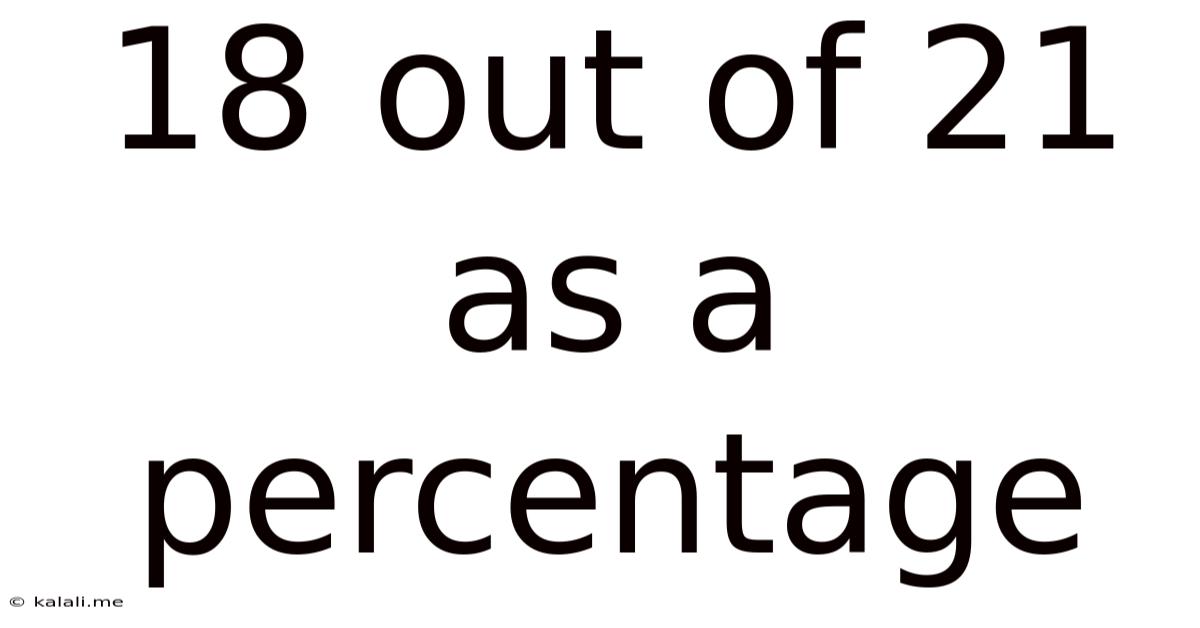
Table of Contents
18 out of 21 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to express fractions as percentages is crucial for clear communication and accurate data interpretation. This comprehensive guide will walk you through calculating "18 out of 21 as a percentage," along with exploring various methods, applications, and related concepts. This will equip you with a strong understanding of percentage calculations and their practical uses.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. It represents a portion or proportion of a whole. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or one-half. Percentages are widely used to express probabilities, rates of change, discounts, and many other proportions. Understanding percentages allows for easy comparison of different proportions, regardless of their initial sizes.
Calculating 18 out of 21 as a Percentage: The Basic Method
The simplest way to calculate 18 out of 21 as a percentage involves two steps:
-
Divide the part by the whole: Divide 18 (the part) by 21 (the whole). This gives you a decimal: 18 ÷ 21 ≈ 0.857
-
Multiply by 100 to convert to a percentage: Multiply the decimal by 100 to express the result as a percentage: 0.857 × 100 = 85.7%
Therefore, 18 out of 21 is approximately 85.7%.
Alternative Methods for Percentage Calculation
While the basic method is straightforward, several other approaches can be used, particularly useful depending on the complexity of the calculation or the tools available.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the process. Simply enter 18 ÷ 21 and then press the % button. The calculator will directly display the percentage.
-
Using a Spreadsheet Program (e.g., Excel, Google Sheets): Spreadsheets offer powerful functions for percentage calculations. The formula
=18/21*100will directly provide the percentage in a spreadsheet cell. -
Using Proportions: This method is helpful for understanding the underlying relationship. Set up a proportion:
18/21 = x/100
Solve for x by cross-multiplying: 21x = 1800
x = 1800/21 ≈ 85.7
Therefore, x ≈ 85.7%, representing the percentage.
Rounding Percentages
In many cases, you'll need to round the percentage to a specific number of decimal places. In the example of 18 out of 21, we rounded to one decimal place (85.7%). The level of rounding depends on the context and the required level of precision. Rounding to the nearest whole number would give 86%. Always consider the context to determine the appropriate level of precision.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world situations:
-
Academic Performance: Calculating grades, test scores, and overall academic performance often involves percentages.
-
Finance and Budgeting: Tracking expenses, calculating savings rates, and understanding interest rates all rely on percentage calculations.
-
Sales and Discounts: Businesses use percentages to advertise discounts, calculate profits, and analyze sales trends.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions, frequencies, and probabilities.
-
Science and Engineering: Percentage calculations are crucial in various scientific fields, including chemistry, physics, and engineering. For instance, calculating concentrations of solutions, efficiency of processes, and error margins often involve percentages.
-
Everyday Life: Percentage calculations are used in tipping at restaurants, calculating sales tax, and understanding growth rates (like population growth).
Understanding Percentage Change
Beyond simply calculating a percentage of a whole, understanding percentage change is equally important. Percentage change measures the relative difference between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a product's price increased from $10 to $12, the percentage change would be:
[(12 - 10) / 10] x 100% = 20%
This indicates a 20% price increase.
Percentage Point vs. Percentage Change
It's crucial to distinguish between "percentage points" and "percentage change." A percentage point refers to an absolute difference between two percentages, while percentage change represents the relative change.
For example, if the interest rate increases from 5% to 8%, the increase is 3 percentage points. However, the percentage change is [(8-5)/5] x 100% = 60%. The difference in terminology is important for accurate communication.
Advanced Percentage Calculations:
-
Calculating the Whole from a Percentage: If you know a percentage of a value and the percentage itself, you can calculate the whole. For example, if 85.7% of a number is 18, the whole number is 18 / (85.7/100) = 21.
-
Compound Percentage Change: This involves calculating percentage change over multiple periods, where each subsequent change is based on the previous period's value. This is common in areas like finance, where interest compounds over time.
-
Weighted Averages: Weighted averages involve assigning different weights to different values before calculating the average, resulting in a more representative outcome. This is particularly useful in situations where different values have varying levels of importance.
Conclusion:
Calculating percentages is a valuable skill with applications across many domains. Mastering basic percentage calculations and understanding related concepts like percentage change and percentage points empowers you to interpret data effectively, solve problems accurately, and communicate information clearly. Whether using the basic formula, a calculator, spreadsheet software, or a proportional method, understanding the principles behind percentage calculations equips you with a crucial skill for navigating numerical information in both professional and personal contexts. The example of 18 out of 21, equating to approximately 85.7%, serves as a simple yet illustrative case study of the power and versatility of percentage calculations. By applying these techniques, you'll be well-prepared to tackle a wide range of percentage-related challenges. Remember to always consider the context and required level of precision when rounding your results.
Latest Posts
Latest Posts
-
How To Get Cube Root On Calculator
Apr 17, 2025
-
How Much Force Is Needed To Accelerate
Apr 17, 2025
-
Least Common Multiple Of 8 And 4
Apr 17, 2025
-
How Many Liters Is 70 Oz
Apr 17, 2025
-
17 3 As A Mixed Number
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 18 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.