2 Is What Percent Of 25
Kalali
Apr 18, 2025 · 5 min read
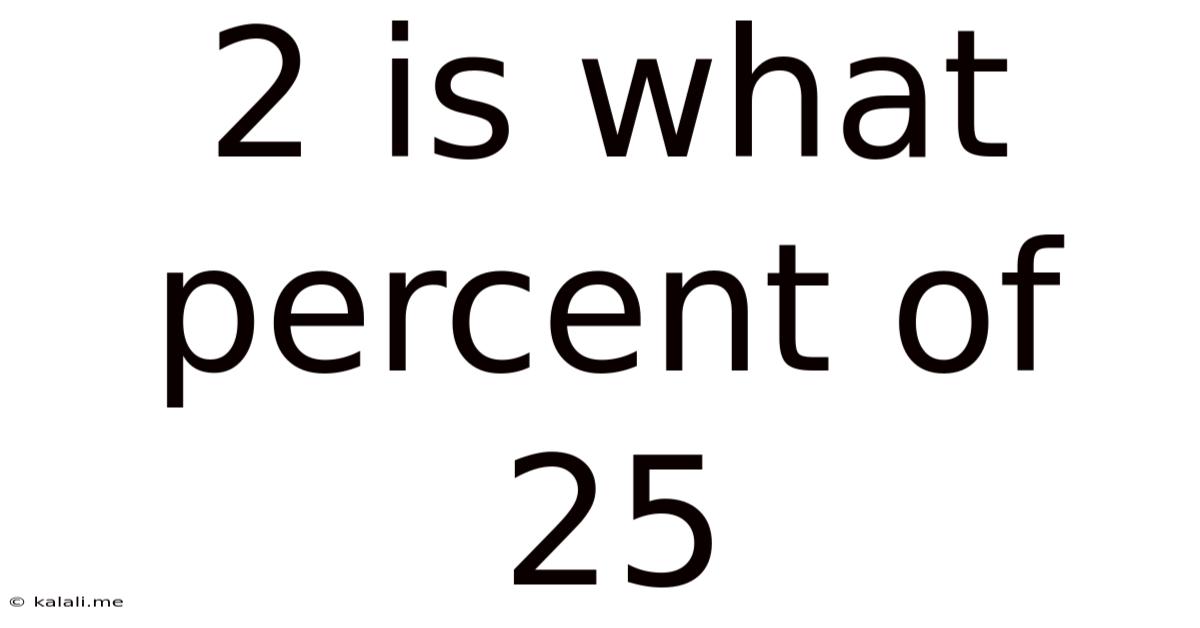
Table of Contents
2 is What Percent of 25? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "2 is what percent of 25?", opens the door to a fascinating world of percentages, their calculations, and their widespread applications in everyday life. Understanding percentages is crucial for navigating finances, interpreting data, and making informed decisions in various fields. This article will not only answer the initial question but also explore the underlying concepts, provide different calculation methods, and illustrate real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to determine what percent 2 is of 25, covering various methods and real-world applications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "per hundred." It's a way to represent a portion of a whole. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Percentages are used extensively to represent proportions, changes, rates, and probabilities in diverse contexts.
Calculating "2 is What Percent of 25?"
There are several ways to solve this problem. Let's explore the most common approaches:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 2
- Whole: 25
Therefore, the calculation is:
(2 / 25) x 100 = 8%
Therefore, 2 is 8% of 25.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion:
- x/100 = 2/25
To solve for x (the percentage), cross-multiply:
25x = 200
x = 200 / 25
x = 8%
This method visually represents the relationship between the parts and the whole, making it easier to understand the underlying logic.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100:
2/25 = 0.08
0.08 x 100 = 8%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous everyday situations. Let's explore some examples:
1. Finance and Budgeting:
- Interest Rates: Banks and financial institutions use percentages to express interest rates on loans, savings accounts, and investments. Understanding interest rates is crucial for making informed financial decisions. For example, a 5% interest rate on a loan means you'll pay 5% of the principal amount as interest.
- Discounts and Sales: Stores frequently advertise discounts as percentages (e.g., "20% off"). Calculating the actual price reduction requires using percentage calculations. If an item costs $50 and is discounted by 20%, the discount is (20/100) * $50 = $10, and the final price is $40.
- Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages. Calculating the amount of tax owed on a purchase or income requires using percentage calculations.
- Tips and Gratuities: Restaurants and service providers often expect tips expressed as a percentage of the total bill. Calculating a 15% or 20% tip on a meal requires accurate percentage calculations.
2. Data Analysis and Statistics:
- Market Share: Businesses use percentages to represent their market share, indicating their proportion of the total market.
- Growth Rates: Companies track percentage growth rates in sales, revenue, and other key metrics to assess their performance.
- Survey Results: Statistical data from surveys and polls are often presented as percentages to show the proportion of respondents holding specific opinions.
- Probability and Statistics: Percentages are essential in expressing probabilities and statistical results.
3. Everyday Life:
- Recipe Scaling: Adjusting recipes to serve more or fewer people requires understanding percentages to scale ingredients proportionally. For example, if a recipe calls for 10% chocolate and you want to double the recipe, you'll need 20% chocolate.
- Grading Systems: Many educational systems use percentages to represent student grades, reflecting their performance on assignments and exams.
- Discounts and Coupons: Understanding percentage discounts on coupons and promotional offers is crucial for saving money.
Advanced Percentage Calculations
While the basic percentage calculation is straightforward, more complex scenarios might require additional steps:
1. Finding the Whole when given the Percentage and Part:
If you know a part and its percentage of the whole, you can determine the whole. For example, if 15% of a number is 30, the whole number can be calculated as:
(30 / 15) x 100 = 200
2. Finding the Percentage Increase or Decrease:
Calculating percentage changes is crucial in comparing values over time. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] x 100
And for percentage decrease:
[(Old Value - New Value) / Old Value] x 100
3. Compound Interest:
Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires understanding exponential growth and involves more complex formulas.
Conclusion
The seemingly simple question, "2 is what percent of 25?", has led us on a journey through the world of percentages, their calculations, and their extensive applications. Mastering percentage calculations is a valuable skill that empowers you to interpret data, manage finances, and make informed decisions in diverse aspects of life. Whether you're calculating discounts, analyzing statistics, or managing your personal finances, the ability to work with percentages is indispensable in the modern world. By understanding the fundamental principles and various methods outlined in this article, you are well-equipped to tackle percentage calculations with confidence and precision. Remember to practice consistently, and you will quickly become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
3 5 Feet Is How Many Inches
Apr 19, 2025
-
3 Out Of 13 As A Percentage
Apr 19, 2025
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.