3 Out Of 13 As A Percentage
Kalali
Apr 19, 2025 · 5 min read
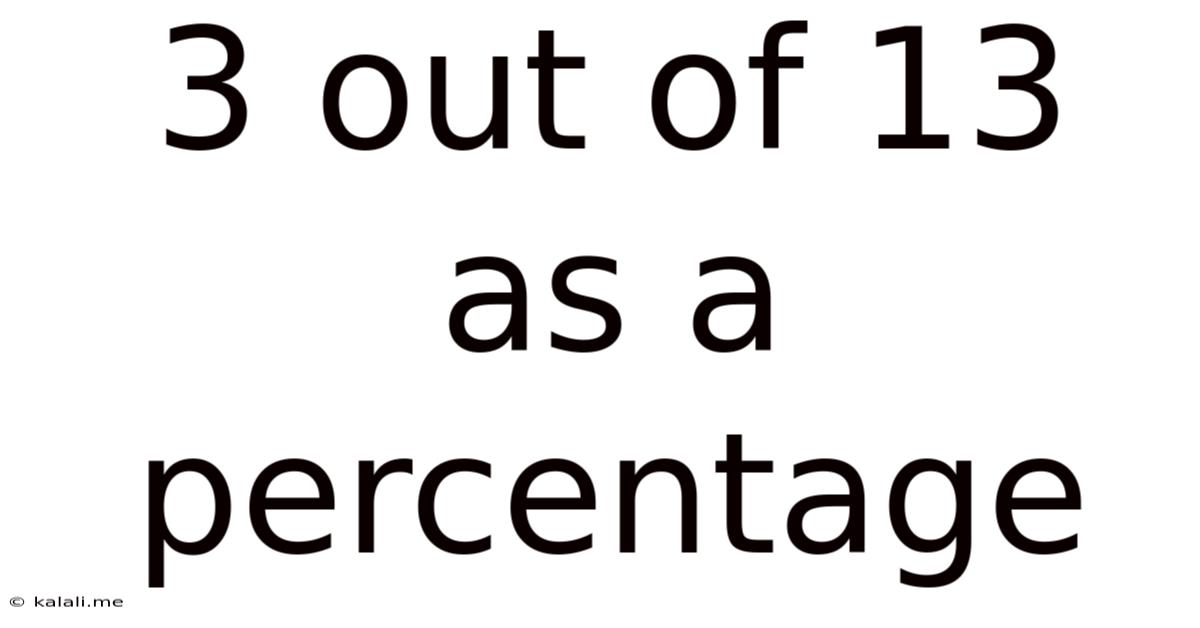
Table of Contents
Decoding 3 out of 13: A Comprehensive Guide to Percentage Calculations and Applications
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article delves deep into the seemingly simple question: "What is 3 out of 13 as a percentage?" We'll not only provide the answer but also explore the underlying principles, different calculation methods, and real-world applications of percentage calculations. This comprehensive guide will empower you with the knowledge to confidently tackle any percentage problem you encounter.
Meta Description: Learn how to calculate 3 out of 13 as a percentage. This in-depth guide covers various calculation methods, practical applications, and explains the underlying mathematical principles for a complete understanding of percentage calculations.
Understanding the Fundamentals of Percentages
Before we dive into the specific calculation, let's establish a solid foundation. A percentage represents a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, expressing a number as a percentage means determining what proportion it represents when the whole is divided into 100 equal parts.
This concept is vital in numerous fields, including:
- Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns.
- Statistics: Representing data visually through charts and graphs, analyzing survey results, and determining probabilities.
- Science: Expressing concentrations of solutions, measuring experimental error, and representing data in scientific papers.
- Everyday life: Understanding sales, comparing prices, and calculating tips.
Calculating 3 out of 13 as a Percentage: Three Different Methods
There are several ways to calculate 3 out of 13 as a percentage. Let's explore three common methods:
Method 1: Using the Fraction Method
This method directly converts the given ratio into a fraction and then multiplies by 100 to express it as a percentage.
-
Represent as a fraction: The statement "3 out of 13" can be written as the fraction 3/13.
-
Convert to decimal: Divide the numerator (3) by the denominator (13): 3 ÷ 13 ≈ 0.2308
-
Multiply by 100: Multiply the decimal by 100 to obtain the percentage: 0.2308 × 100 ≈ 23.08%
Therefore, 3 out of 13 is approximately 23.08%.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve for the percentage.
-
Set up a proportion: We can set up a proportion: 3/13 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply to solve for x: 13x = 300
-
Solve for x: Divide both sides by 13: x = 300/13 ≈ 23.08
Therefore, 3 out of 13 is approximately 23.08%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 3 ÷ 13 and then multiply the result by 100 to obtain the percentage. This is the quickest method for a simple calculation.
Rounding and Precision in Percentage Calculations
The result of 23.08% is an approximation. The actual decimal representation of 3/13 is a repeating decimal (0.230769230769...). The level of precision needed depends on the context. For general purposes, rounding to two decimal places (23.08%) is usually sufficient. However, in contexts requiring high accuracy, such as financial calculations, more decimal places may be necessary.
Real-World Applications of Percentage Calculations: Examples
The ability to calculate percentages is crucial in many real-world scenarios. Let's explore some examples:
1. Sales and Discounts: A store offers a 20% discount on an item originally priced at $100. To calculate the discount, you multiply the original price by the percentage: $100 * 0.20 = $20. The discounted price is $100 - $20 = $80.
2. Tax Calculations: If the sales tax rate is 6%, and the price of an item is $50, the tax amount is $50 * 0.06 = $3. The total cost, including tax, is $50 + $3 = $53.
3. Grade Calculation: A student scores 3 correct answers out of 13 questions on a quiz. As we’ve already calculated, this translates to approximately 23.08%. This percentage can be used to determine the student's grade.
4. Financial Investments: Calculating the return on investment (ROI) involves determining the percentage increase or decrease in the value of an investment. For example, if an investment of $1000 increased to $1200, the ROI is (($1200 - $1000) / $1000) * 100% = 20%.
5. Statistical Analysis: Suppose a survey shows that 3 out of 13 respondents prefer a particular product. This translates to approximately 23.08%, providing valuable insights into consumer preferences.
Beyond the Basics: Advanced Percentage Calculations
While calculating "3 out of 13 as a percentage" is a straightforward example, percentage calculations can become more complex. Here are some advanced concepts:
-
Percentage change: Calculating the percentage increase or decrease between two values. For example, if a value increases from 50 to 60, the percentage increase is ((60-50)/50) * 100% = 20%.
-
Percentage points: This represents the absolute difference between two percentages. For example, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points, not 60%.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest. This is frequently used in finance and loan calculations.
-
Percentage of a percentage: This involves calculating a percentage of a percentage. For instance, finding 10% of 25% of a value requires sequential calculations.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a crucial life skill. This article explored the fundamental principles of percentages, demonstrated various methods for calculating "3 out of 13 as a percentage" (approximately 23.08%), and showcased real-world applications across diverse fields. By mastering these concepts, you’ll be equipped to confidently navigate numerous quantitative situations in your personal and professional life. Remember that understanding the underlying principles is more important than simply memorizing formulas. With practice and a solid grasp of the fundamentals, you can tackle even the most complex percentage problems with ease and accuracy. Remember to always consider the context and round your answers appropriately based on the required level of precision.
Latest Posts
Latest Posts
-
What Is 5 5 In Meters
Apr 20, 2025
-
What Is The Percent Of 1 6
Apr 20, 2025
-
What Percent Of 300 Is 50
Apr 20, 2025
-
How Many Cups Equal 15 Oz
Apr 20, 2025
-
1 Pint Is How Many Milliliters
Apr 20, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 13 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.