What Percent Of 300 Is 50
Kalali
Apr 20, 2025 · 5 min read
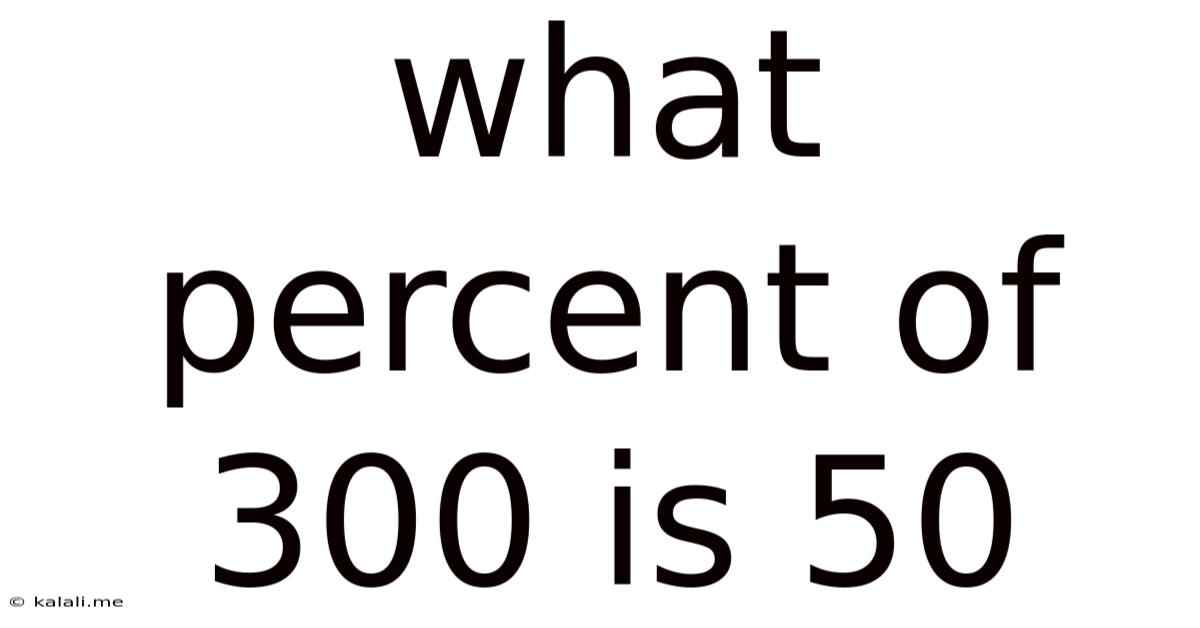
Table of Contents
What Percent of 300 is 50? A Deep Dive into Percentage Calculations
Finding out what percentage 50 represents of 300 might seem like a simple arithmetic problem. However, understanding the underlying principles behind percentage calculations is crucial, not just for solving this specific problem, but for a wide range of applications in daily life, from calculating discounts and sales tax to understanding statistical data and financial reports. This article will provide a comprehensive explanation of how to calculate percentages, focusing on the example of "What percent of 300 is 50?", and will delve into various methods and practical applications. This guide will also explore advanced concepts related to percentage calculations and provide some tips for improving your proficiency. Ultimately, you'll not only understand the answer to the title question but also gain a solid understanding of percentage calculations in general.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal. Percentages are a common way to express proportions, rates, and changes in various contexts. They provide a standardized way to compare different quantities and easily visualize portions of a whole.
Method 1: Using the Proportion Method
This is arguably the most straightforward method for calculating percentages. We can set up a proportion to solve the problem:
- Part/Whole = Percentage/100
In our case:
- Part = 50
- Whole = 300
- Percentage = x (what we need to find)
Substituting these values into the proportion equation:
- 50/300 = x/100
To solve for x, we can cross-multiply:
- 50 * 100 = 300 * x
- 5000 = 300x
Now, divide both sides by 300 to isolate x:
- x = 5000 / 300
- x = 16.67 (approximately)
Therefore, 50 is approximately 16.67% of 300.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying.
First, we express the relationship as a fraction:
- 50/300
Next, we divide the numerator (50) by the denominator (300):
- 50 ÷ 300 = 0.1667 (approximately)
Finally, to convert this decimal to a percentage, we multiply by 100:
- 0.1667 * 100 = 16.67%
This confirms our result from the proportion method. This method is particularly useful when working with calculators, as it minimizes the number of steps.
Method 3: Using the Formula: (Part/Whole) * 100
This is a concise formula that directly calculates the percentage. Simply plug in the values:
- (50/300) * 100 = 16.67%
This formula combines the steps of the decimal method into a single calculation. It's a quick and efficient way to find the percentage.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world scenarios. Here are just a few examples:
- Sales and Discounts: Calculating the final price after a discount (e.g., 20% off a $100 item).
- Taxes: Determining the amount of sales tax or income tax payable.
- Tips and Gratuities: Calculating the appropriate tip amount in a restaurant.
- Finance: Understanding interest rates, loan repayments, and investment returns.
- Statistics: Interpreting data presented as percentages in surveys, polls, and reports. Understanding statistical significance often involves percentage calculations.
- Data Analysis: Representing proportions of data sets and visualizing trends.
- Profit Margins: In business, calculating profit margins involves determining the percentage of revenue that represents profit.
- Grade Calculations: Converting raw scores on tests to percentages.
- Recipe Scaling: Adjusting ingredient quantities in recipes based on the desired yield (percentage increase or decrease).
Beyond the Basics: Advanced Percentage Concepts
While the above methods cover the fundamental aspects of percentage calculations, several more complex scenarios require a deeper understanding.
- Percentage Increase and Decrease: These calculations involve determining the percentage change between two values. For example, if a price increases from $100 to $120, the percentage increase is 20%.
- Compounding Percentages: This refers to the effect of repeatedly applying a percentage change over time. It's commonly used in finance to calculate compound interest.
- Percentage Points: It's crucial to distinguish between percentage points and percentage change. For instance, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
- Weighted Averages: When dealing with multiple percentages that contribute differently to a total, weighted averages are necessary. This is common in calculating GPA (Grade Point Average).
Improving Your Percentage Calculation Skills
Here are some tips to enhance your proficiency in percentage calculations:
- Practice Regularly: The more you practice, the more comfortable and efficient you'll become.
- Use Different Methods: Experiment with the various methods described in this article to find the approach that suits you best.
- Check Your Work: Always verify your results to ensure accuracy. Use a calculator to cross-check your manual calculations.
- Understand the Concepts: Focus on understanding the underlying principles of percentages rather than simply memorizing formulas.
- Utilize Online Calculators: Many online calculators can assist in percentage calculations, particularly for complex scenarios. However, understanding the process is always more important than relying solely on a tool.
Conclusion:
In conclusion, 50 is approximately 16.67% of 300. This seemingly simple calculation underlines the importance of understanding percentage computations. Whether you're dealing with everyday tasks or complex financial analysis, a solid grasp of percentage calculations is an invaluable skill. By mastering the methods outlined in this article and practicing regularly, you can confidently tackle various percentage problems and effectively utilize this fundamental mathematical concept in numerous real-world situations. Remember that accuracy and understanding the underlying concepts are key to successfully applying percentage calculations.
Latest Posts
Latest Posts
-
Where Should Glass Slides Pipettes And Capillary Tubes Be Disposed
Apr 22, 2025
-
Convert 48 Degrees Farenheit To Celcius
Apr 22, 2025
-
How Many Liters Is 7 Gallons
Apr 22, 2025
-
How To Turn 2 5 8 Into A Decimal
Apr 22, 2025
-
What Is 17 12 As A Mixed Number
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 300 Is 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.