What Is 17/12 As A Mixed Number
Kalali
Apr 22, 2025 · 5 min read
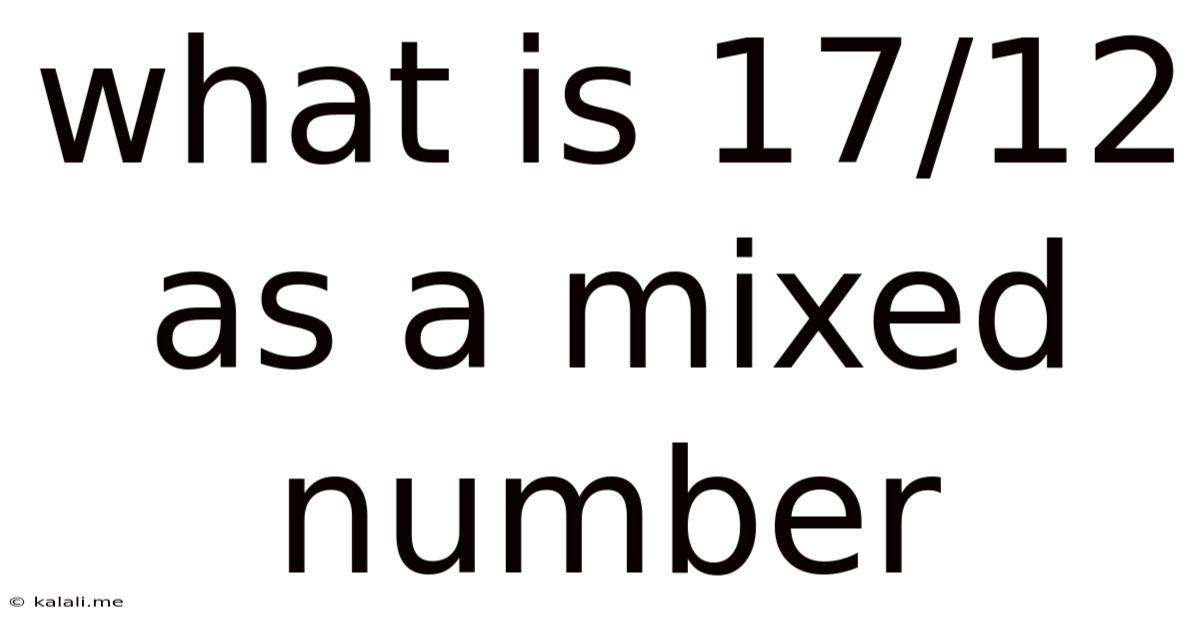
Table of Contents
What is 17/12 as a Mixed Number? A Comprehensive Guide to Fraction Conversion
Understanding fractions and their various forms is fundamental to mathematics. This article delves deep into the process of converting an improper fraction, like 17/12, into a mixed number. We'll not only show you how to do it but also explore the underlying concepts, offer practical examples, and provide you with the tools to confidently tackle similar fraction conversions. This guide is perfect for students learning fractions, teachers needing supplementary materials, or anyone looking to refresh their mathematical skills.
Meta Description: Learn how to convert the improper fraction 17/12 into a mixed number. This comprehensive guide provides a step-by-step process, explanations, examples, and explores the underlying concepts of fractions. Master fraction conversion today!
Understanding Fractions: A Quick Refresher
Before diving into the conversion, let's quickly review the basics. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
There are three main types of fractions:
- Proper Fraction: The numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8). The value of a proper fraction is always less than 1.
- Improper Fraction: The numerator is equal to or larger than the denominator (e.g., 7/4, 5/5, 17/12). The value of an improper fraction is always greater than or equal to 1.
- Mixed Number: Combines a whole number and a proper fraction (e.g., 1 3/4, 2 1/2, 3 5/8). It represents a value greater than 1.
Converting 17/12 to a Mixed Number: A Step-by-Step Approach
The fraction 17/12 is an improper fraction because the numerator (17) is greater than the denominator (12). To convert it to a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is. Here's the process:
Step 1: Perform the Division
Divide the numerator (17) by the denominator (12).
17 ÷ 12 = 1 with a remainder of 5
Step 2: Identify the Whole Number
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
Step 3: Identify the Fraction
The remainder (the amount left over after the division) becomes the numerator of the fraction in the mixed number. The denominator remains the same as the original fraction. So, the remainder is 5, and the denominator is 12. This gives us the fraction 5/12.
Step 4: Combine the Whole Number and Fraction
Combine the whole number from Step 2 and the fraction from Step 3 to form the mixed number.
Therefore, 17/12 as a mixed number is 1 5/12.
Visualizing the Conversion
Imagine you have 17 slices of pizza, and each pizza has 12 slices. You can form one complete pizza (12 slices) and have 5 slices left over. This visually represents the mixed number 1 5/12.
More Examples of Improper Fraction to Mixed Number Conversion
Let's practice with a few more examples to solidify our understanding:
-
Convert 22/5 to a mixed number:
22 ÷ 5 = 4 with a remainder of 2. Therefore, 22/5 = 4 2/5
-
Convert 19/6 to a mixed number:
19 ÷ 6 = 3 with a remainder of 1. Therefore, 19/6 = 3 1/6
-
Convert 35/8 to a mixed number:
35 ÷ 8 = 4 with a remainder of 3. Therefore, 35/8 = 4 3/8
-
Convert 27/4 to a mixed number:
27 ÷ 4 = 6 with a remainder of 3. Therefore, 27/4 = 6 3/4
Converting Mixed Numbers to Improper Fractions: The Reverse Process
It's often helpful to be able to convert in both directions. To convert a mixed number back into an improper fraction, follow these steps:
- Multiply the whole number by the denominator: Multiply the whole number part of the mixed number by the denominator of the fraction.
- Add the numerator: Add the result from step 1 to the numerator of the fraction.
- Keep the denominator: The denominator remains the same.
Let's convert our example, 1 5/12, back to an improper fraction:
- 1 (whole number) x 12 (denominator) = 12
- 12 + 5 (numerator) = 17
- The denominator remains 12.
Therefore, 1 5/12 = 17/12.
Practical Applications of Fraction Conversion
The ability to convert between improper fractions and mixed numbers is crucial in various mathematical contexts and real-world situations:
- Baking and Cooking: Recipes often use mixed numbers for ingredient quantities. Converting them to improper fractions can be helpful for precise measurements.
- Construction and Engineering: Precise calculations involving fractions are essential in construction and engineering. Converting between fraction forms allows for efficient calculations.
- Data Analysis: In data analysis and statistics, understanding and manipulating fractions are crucial for accurate interpretation and reporting of findings.
- Everyday Life: Dividing things fairly, sharing resources, or calculating parts of a whole often involves fractions. Converting between different fraction forms helps in these situations.
Advanced Concepts and Further Exploration
While this article focused on the fundamental conversion between improper fractions and mixed numbers, further exploration can involve:
- Simplifying Fractions: Reducing fractions to their simplest form by finding the greatest common divisor (GCD) of the numerator and denominator.
- Adding, Subtracting, Multiplying, and Dividing Fractions: Mastering these operations is crucial for advanced mathematical problem-solving.
- Working with Decimals: Converting fractions to decimals and vice versa enhances mathematical flexibility.
Conclusion
Converting an improper fraction, such as 17/12, into a mixed number is a fundamental skill in mathematics. By understanding the underlying concepts and following the step-by-step process outlined in this article, you can confidently perform this conversion and apply it to various mathematical and real-world situations. Remember to practice regularly to build your proficiency and expand your understanding of fractions. Mastering this skill will undoubtedly improve your mathematical abilities and problem-solving skills. So, grab your pencil, practice these conversions, and watch your fractional understanding grow!
Latest Posts
Latest Posts
-
How Many Hours Is 192 Minutes
Apr 22, 2025
-
What Is 80 Degrees In Celsius
Apr 22, 2025
-
How Long Do Dust Storms Last
Apr 22, 2025
-
25 Is What Percent Of 20
Apr 22, 2025
-
Cuanto Son 10 Millas En Kilometros
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 17/12 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.