2 Of 7 Is What Percent
Kalali
Apr 15, 2025 · 5 min read
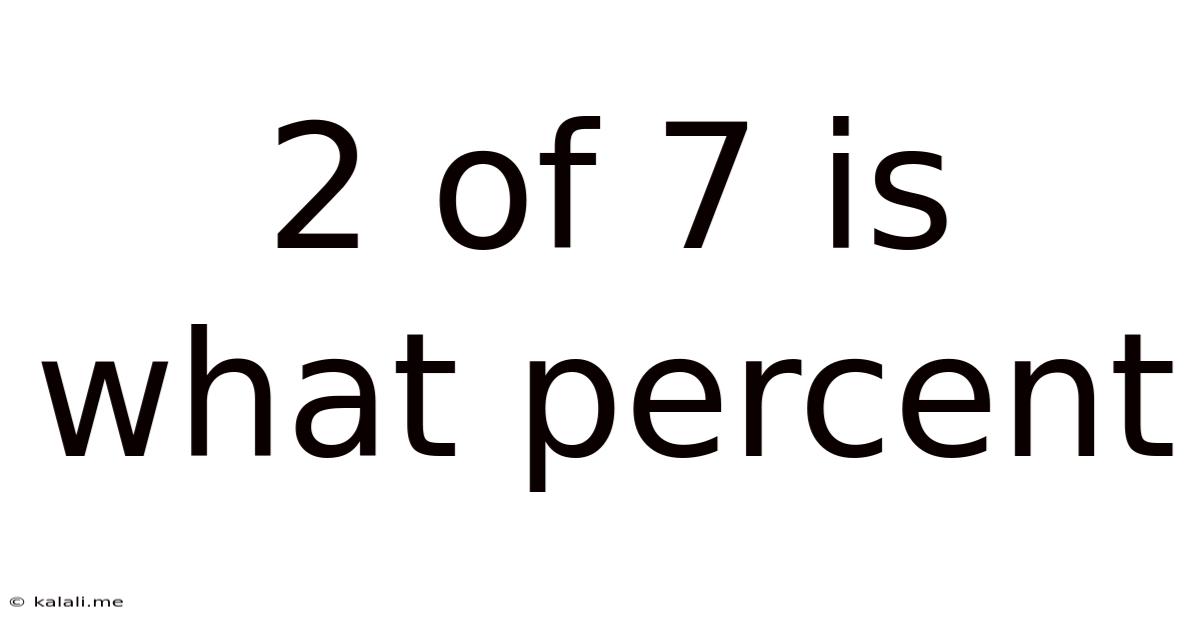
Table of Contents
2 out of 7 is What Percent? A Comprehensive Guide to Percentage Calculations
Finding percentages is a fundamental skill applicable in countless daily situations, from calculating discounts and sales tax to understanding statistics and financial reports. This article delves deep into the calculation of "2 out of 7 is what percent?", explaining the process step-by-step, exploring different calculation methods, and providing practical applications and real-world examples. We'll also discuss related percentage problems and explore how to improve your understanding of percentages. This comprehensive guide will equip you with the knowledge and tools to confidently tackle any percentage calculation.
What is a Percentage?
Before diving into the calculation, let's define what a percentage actually is. A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
Calculating "2 out of 7 is What Percent?"
There are several ways to calculate what percentage 2 out of 7 represents. Let's explore the most common methods:
Method 1: The Fraction-to-Decimal-to-Percentage Method
-
Express as a fraction: The problem "2 out of 7" is easily represented as the fraction 2/7.
-
Convert the fraction to a decimal: Divide the numerator (2) by the denominator (7). 2 ÷ 7 ≈ 0.2857
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add a percentage sign (%). 0.2857 × 100 ≈ 28.57%
Therefore, 2 out of 7 is approximately 28.57%.
Method 2: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion where x represents the percentage we are trying to find:
2/7 = x/100
To solve for x, cross-multiply:
7x = 200
Divide both sides by 7:
x = 200/7 ≈ 28.57
Therefore, x ≈ 28.57%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 2 by 7 and then multiply the result by 100 to obtain the percentage. This is the quickest and most efficient method, especially for more complex percentage calculations.
Rounding and Precision
Notice that in the calculations above, we obtained an approximate answer of 28.57%. The actual result is a repeating decimal (0.2857142857...). The level of precision required depends on the context. In many cases, rounding to two decimal places (28.57%) is sufficient. However, in situations requiring higher accuracy, you might need to use more decimal places or express the answer as a fraction.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Sales and Discounts: Calculating discounts offered on products or services. For example, a 20% discount on a $100 item means a savings of $20.
-
Taxes: Determining the amount of sales tax or income tax owed.
-
Financial Analysis: Analyzing financial statements, such as calculating profit margins, return on investment (ROI), and interest rates.
-
Statistics: Interpreting statistical data, such as percentages in polls, surveys, and research studies.
-
Grading Systems: Calculating grades in educational settings based on scores achieved on assignments and exams.
-
Probability: Determining the probability of events occurring, often expressed as percentages. For example, the probability of getting heads when flipping a coin is 50%.
-
Recipe Scaling: Adjusting recipe ingredients based on the number of servings required.
Expanding on Percentage Problems: Related Concepts
The fundamental understanding of calculating percentages allows you to tackle more complex problems:
-
Finding the Whole: If 28.57% of a number is 2, what is the whole number? This requires using the formula: Whole = Part / (Percentage/100). In this case, the whole number is approximately 7.
-
Finding the Part: If 15% of a number is 3, what is 15% of the number? This is a straightforward percentage calculation: Part = (Percentage/100) * Whole.
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two numbers. For instance, if a price increases from $50 to $60, the percentage increase is calculated as: [(New Value - Old Value) / Old Value] * 100%.
-
Percentage Change: This calculation determines the percentage difference between two values, regardless of whether it's an increase or a decrease. The formula is similar to percentage increase/decrease, but the result can be negative, indicating a decrease.
Improving Your Percentage Calculation Skills
Here are some tips to enhance your understanding and proficiency in percentage calculations:
-
Practice regularly: The more you practice, the more comfortable and efficient you'll become. Solve various percentage problems from different sources to strengthen your understanding.
-
Use visual aids: Diagrams, charts, and graphs can help visualize percentage relationships and make calculations easier to understand.
-
Understand the underlying concepts: Don't just memorize formulas; understand the logic and reasoning behind each calculation.
-
Utilize online resources: There are numerous online calculators, tutorials, and practice exercises available to assist your learning.
-
Break down complex problems: Divide complex percentage problems into smaller, manageable steps to avoid errors.
-
Check your work: Always verify your calculations to ensure accuracy. Use alternative methods to cross-check your results.
Conclusion
Calculating percentages is a vital skill with widespread applications in various aspects of life. Understanding the different methods for solving percentage problems, such as the fraction-to-decimal-to-percentage method, the proportion method, and using a calculator, allows you to approach these calculations confidently and accurately. By practicing regularly and focusing on the underlying concepts, you can master percentage calculations and apply this essential skill to real-world situations, from everyday shopping to complex financial analysis. Remember that accuracy is crucial, especially in contexts like finance and statistics. Always double-check your work and choose the appropriate level of precision for the specific problem you're solving. With consistent practice and a strong understanding of the fundamentals, you'll become adept at solving any percentage-related problem.
Latest Posts
Latest Posts
-
Why Is The Product Of Saponification A Salt
Apr 16, 2025
-
What Is 15 Out Of 20 As A Percentage
Apr 16, 2025
-
Cuanto Es 90 Pulgadas En Centimetros
Apr 16, 2025
-
Cuantos Grados Centigrados Son 61 Fahrenheit
Apr 16, 2025
-
Can Travel Through A Empty Space
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 2 Of 7 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.