20 8 As A Mixed Number
Kalali
Apr 06, 2025 · 4 min read
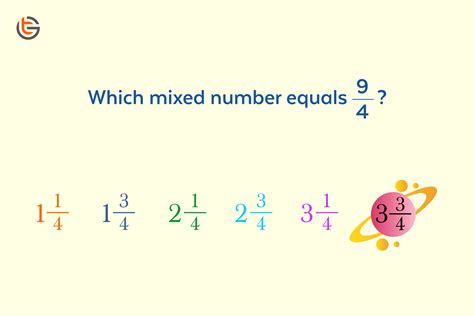
Table of Contents
20/8 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversions is fundamental in mathematics. This article delves deep into converting the improper fraction 20/8 into a mixed number, explaining the process step-by-step and exploring related concepts to solidify your understanding. We'll cover various methods, address common mistakes, and provide ample practice examples. By the end, you'll be confident in handling similar fraction conversions.
What is a Mixed Number?
Before we dive into the conversion, let's define what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number, comprising the whole number 2 and the proper fraction ¾.
Converting 20/8 to a Mixed Number: The Division Method
The most straightforward method for converting an improper fraction (where the numerator is larger than or equal to the denominator) like 20/8 into a mixed number involves division.
Step 1: Divide the Numerator by the Denominator
Divide the numerator (20) by the denominator (8).
20 ÷ 8 = 2 with a remainder of 4
Step 2: Identify the Whole Number and the Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 2. The remainder (the number left over after the division) becomes the numerator of the proper fraction. Our remainder is 4.
Step 3: Form the Mixed Number
The denominator of the fraction remains the same as the original improper fraction's denominator (8). Therefore, we combine the whole number and the fraction to form the mixed number:
20/8 = 2 ⁴⁄₈
Simplifying the Fraction
Notice that the fraction ⁴⁄₈ can be simplified. Both the numerator and the denominator share a common factor of 4. Simplifying the fraction means dividing both the numerator and the denominator by their greatest common divisor (GCD).
⁴⁄₈ ÷ ⁴⁄₄ = ¹⁄₂
Therefore, the simplified mixed number is:
20/8 = 2 ¹⁄₂
Alternative Methods: Understanding the Underlying Concept
While the division method is the most efficient, understanding the underlying concept can enhance your grasp of fractions. Let's explore an alternative approach.
Method 2: Breaking Down the Improper Fraction
We can rewrite the improper fraction 20/8 as a sum of proper fractions and whole numbers.
20/8 can be thought of as:
8/8 + 8/8 + 4/8
Since 8/8 equals 1, we can simplify this to:
1 + 1 + ⁴⁄₈ = 2 ⁴⁄₈
Again, simplifying the fraction gives us the final answer:
2 ¹⁄₂
Common Mistakes to Avoid
Several common mistakes can occur when converting improper fractions to mixed numbers. Let's address them:
- Forgetting to Simplify: Always check if the resulting fraction in your mixed number can be simplified. Failing to simplify is a frequent oversight.
- Incorrect Division: Ensure you perform the division correctly. A wrong quotient or remainder will lead to an incorrect mixed number.
- Misplacing the Remainder: Remember that the remainder becomes the numerator of the fraction in the mixed number. Confusing the remainder with the quotient is a common mistake.
- Ignoring the Denominator: The denominator remains unchanged throughout the conversion process. Don't forget to keep the original denominator.
Practice Problems
Let's solidify your understanding with some practice problems. Convert the following improper fractions to mixed numbers, simplifying where possible:
- 15/4
- 22/5
- 31/6
- 100/12
- 45/9
Solutions:
- 15/4 = 3 ¾
- 22/5 = 4 ²⁄₅
- 31/6 = 5 ¹⁄₆
- 100/12 = 8 ⁴⁄₁₂ = 8 ¹⁄₃ (Remember to simplify!)
- 45/9 = 5 (This one is a whole number, no fraction required)
Beyond the Basics: Real-World Applications
Converting improper fractions to mixed numbers isn't just an academic exercise; it has numerous real-world applications.
- Cooking and Baking: Recipes often use fractions, and understanding mixed numbers allows for accurate measurements.
- Construction and Engineering: Precise measurements in construction rely on fraction understanding. Converting improper fractions to mixed numbers aids in accurate calculations.
- Sewing and Tailoring: Pattern making and garment construction often involve fractional measurements.
- Data Analysis: When working with datasets, you might encounter fractions that need to be converted for better interpretation.
Conclusion
Converting an improper fraction like 20/8 to a mixed number is a fundamental mathematical skill with wide-ranging applications. By mastering the division method and understanding the underlying concepts, you can confidently tackle fraction conversions and apply this knowledge to various real-world scenarios. Remember to always simplify your fractions for the most accurate and concise representation. Practice regularly to build your proficiency and confidence in working with fractions. With consistent effort, you'll find that fractions become much less daunting and more intuitive.
Latest Posts
Latest Posts
-
What Is 75 Percent Of 15
Apr 08, 2025
-
How Many Grams Is 3000 Milligrams
Apr 08, 2025
-
Is Luster A Chemical Or Physical Property
Apr 08, 2025
-
5 Foot 5 Inches In Meters
Apr 08, 2025
-
How Long Is 2 Meters In Inches
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about 20 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.