What Is 75 Percent Of 15
Kalali
Apr 08, 2025 · 5 min read
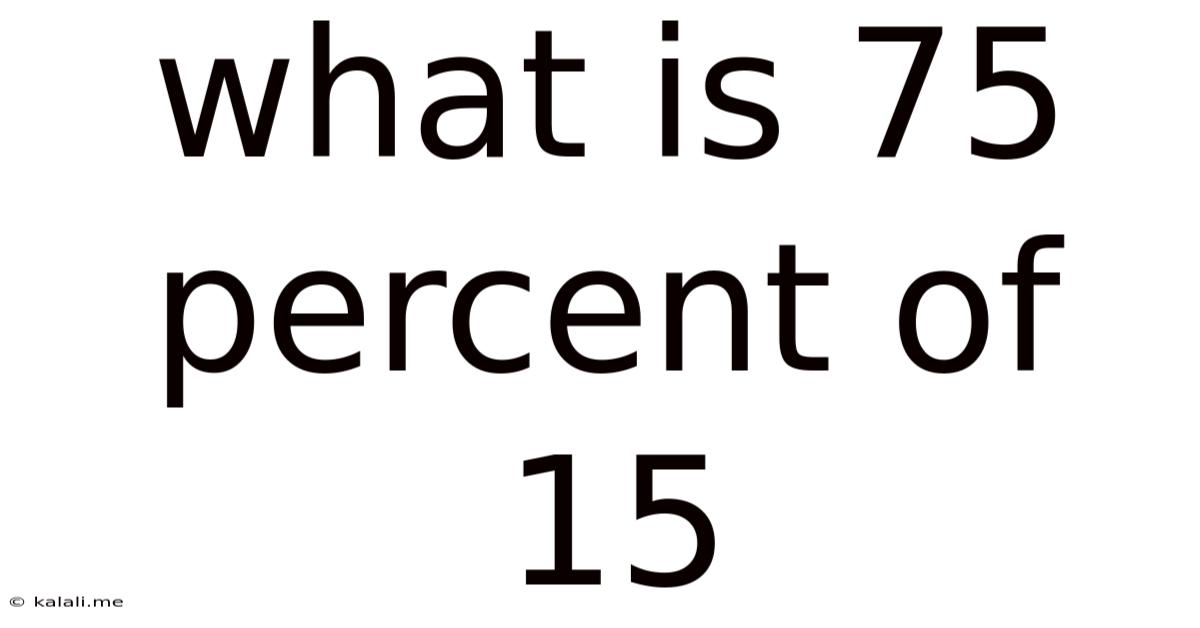
Table of Contents
What is 75 Percent of 15? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "What is 75 percent of 15?", opens the door to a broader understanding of percentages, their calculations, and their widespread applications in various fields. While the answer itself is easily obtainable through a quick calculation, exploring the underlying concepts provides invaluable knowledge for everyday life and professional endeavors. This article will not only provide the solution but delve deep into the methods, practical examples, and the importance of understanding percentages.
Meta Description: Discover how to calculate 75% of 15 and explore the world of percentages. Learn different calculation methods, real-world applications, and the significance of percentage understanding in various fields. This comprehensive guide covers everything from basic arithmetic to advanced percentage-related problems.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentages. Essentially, a percentage represents a portion or proportion of a whole. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Understanding this fundamental concept is crucial before tackling any percentage calculation.
Calculating 75% of 15: Three Different Approaches
There are several ways to calculate 75% of 15. Let's explore three common methods:
1. The Fraction Method:
This method leverages the fact that 75% can be expressed as a fraction: 75/100, which simplifies to ¾. Therefore, calculating 75% of 15 is the same as calculating ¾ of 15:
(¾) * 15 = (3/4) * 15 = 45/4 = 11.25
2. The Decimal Method:
This method converts the percentage to its decimal equivalent. 75% is equal to 0.75 (75 divided by 100). Then, multiply this decimal by 15:
0.75 * 15 = 11.25
3. The Percentage Formula:
The general formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
Applying this to our problem:
(75/100) * 15 = 11.25
Therefore, 75% of 15 is 11.25.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-life situations. Here are some examples:
- Shopping and Sales: Calculating discounts during sales is a common application. If a shirt is 20% off its original price of $50, you'd calculate 20% of $50 to determine the discount amount ($10).
- Finance and Investments: Understanding interest rates, returns on investments, and loan repayments often requires percentage calculations. For example, calculating the interest earned on a savings account or determining the monthly payment on a mortgage involves percentages.
- Taxes: Calculating income tax, sales tax, and other taxes requires a strong understanding of percentages. Tax rates are typically expressed as percentages of income or purchase price.
- Statistics and Data Analysis: Percentages are extensively used to represent data and proportions in various fields like demographics, market research, and scientific studies.
- Healthcare: Percentages are used in many medical contexts, such as calculating dosage amounts, determining the effectiveness of treatments, and analyzing medical data.
- Cooking and Baking: Adjusting recipes based on different quantities often involves using percentages to maintain the correct proportions of ingredients. For example, if a recipe calls for 10% of an ingredient compared to another, you need to be able to work this out.
- Education: Grading systems, test scores, and performance evaluations frequently use percentages to represent achievements.
- Sports: Statistics in sports like batting averages, winning percentages, and free throw percentages rely heavily on percentage calculations.
These examples illustrate the versatility of percentage calculations and their importance in various aspects of our lives.
Advanced Percentage Problems and Concepts
While calculating 75% of 15 is straightforward, more complex problems can arise. Here are some advanced concepts:
- Finding the Percentage: Instead of finding a percentage of a number, you might need to determine what percentage one number represents of another. For example, what percentage is 12 of 60? (Answer: 20%). This involves dividing the smaller number by the larger number and multiplying by 100.
- Finding the Original Number: You might know the percentage and the resulting value, but need to find the original number. For example, if 25% of a number is 10, what is the original number? (Answer: 40). This involves setting up an equation and solving for the unknown.
- Percentage Change: Calculating percentage increase or decrease is common. For example, if a stock price rises from $10 to $12, what is the percentage increase? (Answer: 20%). This involves finding the difference, dividing it by the original value, and multiplying by 100.
- Compound Interest: This is a more complex scenario where interest is earned not only on the principal amount but also on accumulated interest. Understanding compound interest requires a firm grasp of percentage calculations and exponential growth.
Mastering these advanced concepts requires a solid foundation in basic percentage calculations.
Tips and Tricks for Efficient Percentage Calculations
- Memorize common percentage equivalents: Knowing that 50% = 0.5, 25% = 0.25, and 75% = 0.75 can significantly speed up calculations.
- Use estimation: For quick estimations, round numbers to make the calculations easier.
- Employ mental math techniques: Practice mental math strategies to perform calculations more efficiently.
- Use calculators or spreadsheet software: For more complex calculations, utilize calculators or spreadsheet software to ensure accuracy.
- Practice regularly: Consistent practice is key to mastering percentage calculations and applying them effectively.
Conclusion: The Importance of Understanding Percentages
The seemingly simple question of "What is 75 percent of 15?" reveals the underlying importance of understanding percentages. From everyday shopping to complex financial calculations, percentages are ubiquitous. Mastering percentage calculations enhances problem-solving skills, facilitates better decision-making, and improves comprehension in various fields. This comprehensive guide has aimed to provide not just the answer but a deep understanding of the concepts, methods, and applications of percentages. Remember to practice regularly and embrace the versatility of this fundamental mathematical tool. By understanding percentages, you equip yourself with a valuable skill applicable throughout your life.
Latest Posts
Latest Posts
-
What Are The Monomers Of Dna
Apr 17, 2025
-
How Many Kilos Is 17 Pounds
Apr 17, 2025
-
2 Km Is How Many Meters
Apr 17, 2025
-
What Is The Fraction Of 1 6
Apr 17, 2025
-
What Percentage Of 16 Is 10
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.