20 As A Percentage Of 50
Kalali
Mar 09, 2025 · 5 min read
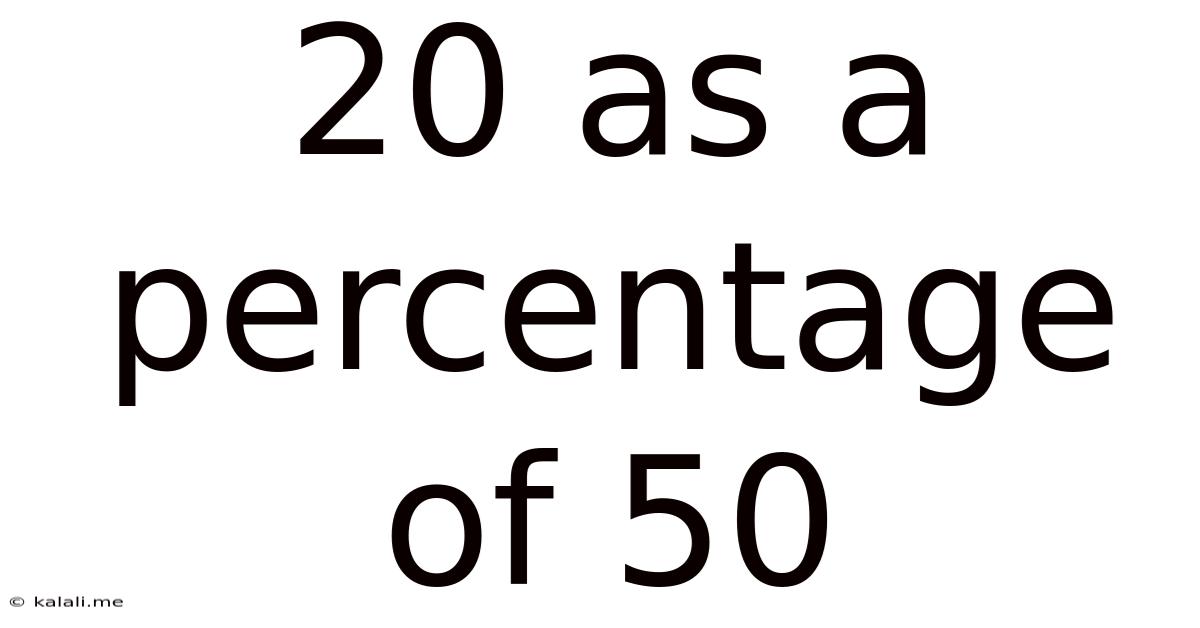
Table of Contents
20 as a Percentage of 50: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine one number as a percentage of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide delves into the calculation of 20 as a percentage of 50, explaining the process step-by-step and exploring related concepts to enhance your understanding of percentage calculations.
Understanding Percentages
Before we dive into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 20% means 20 out of 100, or 20/100. This can be simplified to 1/5.
Percentages provide a standardized way to compare proportions and understand relative quantities. They are used extensively in various fields, including:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data, analyzing trends, and making inferences.
- Science: Expressing concentrations, errors, and experimental results.
- Everyday Life: Understanding sales, tips, and proportions in recipes.
Calculating 20 as a Percentage of 50: The Step-by-Step Method
To calculate 20 as a percentage of 50, we follow these simple steps:
Step 1: Set up the Fraction
First, express the relationship between the two numbers as a fraction. In this case, 20 is the part, and 50 is the whole. So, the fraction is 20/50.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (20) by the denominator (50):
20 ÷ 50 = 0.4
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.4 × 100 = 40%
Therefore, 20 is 40% of 50.
Alternative Methods for Calculating Percentages
While the above method is the most straightforward, there are alternative approaches you can use to calculate percentages:
Using Proportions
You can solve this problem using proportions. We can set up a proportion:
20/50 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
50x = 2000
x = 2000/50
x = 40
Therefore, x = 40%, confirming our previous result.
Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
Substituting our values:
(20 / 50) * 100 = 40%
This formula provides a concise and efficient method for calculating percentages.
Real-World Applications of Percentage Calculations
Understanding percentage calculations has numerous practical applications in daily life. Here are a few examples:
-
Sales and Discounts: If a store offers a 40% discount on an item originally priced at $50, you can quickly calculate the discount amount ($20) and the final price ($30) using the percentage calculations we've discussed.
-
Taxes: Calculating sales tax or income tax involves understanding percentages. For instance, if the sales tax rate is 6%, you can determine the tax amount on a purchase by multiplying the purchase price by 0.06.
-
Tips: Calculating a tip in a restaurant usually involves determining a percentage of the total bill. A 15% tip on a $50 meal would be $7.50.
-
Financial Investments: Understanding percentage changes in stock prices or investment returns is crucial for making informed financial decisions.
-
Grade Calculations: Many academic grading systems use percentages to represent a student's performance in a course.
-
Scientific Measurements: Scientists frequently use percentages to express the concentration of substances in solutions, the accuracy of measurements, and the error rates in experiments.
Beyond the Basics: More Complex Percentage Problems
While calculating 20 as a percentage of 50 is a relatively simple problem, understanding percentages extends to more complex scenarios:
-
Finding the Whole: If you know the part and the percentage, you can calculate the whole. For example, if 40% of a number is 20, then the number is 50 (20 / 0.4 = 50).
-
Finding the Part: If you know the whole and the percentage, you can calculate the part. For example, 40% of 50 is 20 (0.4 * 50 = 20).
-
Percentage Increase/Decrease: Calculating percentage increases or decreases is crucial for tracking changes over time. For example, if a value increases from 50 to 70, the percentage increase is 40% ((70-50)/50 * 100 = 40%).
-
Compound Interest: Compound interest calculations involve repeated percentage calculations to determine the future value of an investment.
Mastering Percentage Calculations: Tips and Tricks
To become proficient in percentage calculations, consider the following tips:
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Solve various percentage problems to build your understanding and speed.
-
Use Visual Aids: Charts, graphs, and diagrams can help visualize percentages and make them easier to understand.
-
Utilize Calculators and Software: Calculators and software programs can simplify complex percentage calculations and save you time.
-
Understand the Context: Always pay attention to the context of the problem. Understanding the meaning of the numbers and the question being asked is crucial for accurate calculations.
-
Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, manageable steps.
-
Check Your Work: Always double-check your answers to ensure accuracy.
Conclusion: The Importance of Percentage Calculations
Understanding and applying percentage calculations is an essential life skill. From making informed financial decisions to interpreting data in various contexts, the ability to calculate percentages accurately and efficiently is invaluable. The simple calculation of 20 as a percentage of 50 serves as a foundational example, illustrating the core principles and steps involved in this crucial mathematical skill. By mastering these principles and practicing regularly, you will enhance your numerical literacy and improve your ability to navigate the quantitative aspects of your daily life. Remember to utilize various methods and apply your knowledge to real-world scenarios to solidify your understanding and build confidence in your percentage calculation abilities.
Latest Posts
Latest Posts
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
-
How Many Centimeters Are In A Meter Stick
Jul 10, 2025
-
Why Did The Orchestra Get An R Rating
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 20 As A Percentage Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.