20 Is What Percent Of 25
Kalali
Apr 12, 2025 · 5 min read
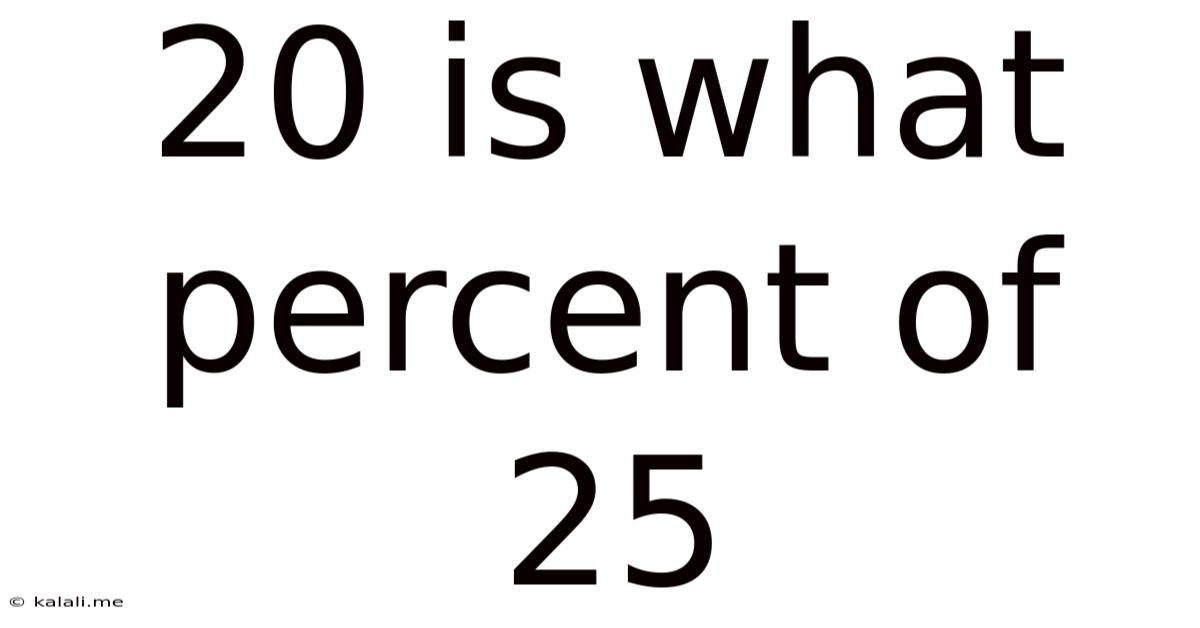
Table of Contents
20 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "20 is what percent of 25?", opens the door to a broader understanding of percentages, their applications, and how to solve various percentage-related problems. This article will not only answer the question directly but also delve into the underlying mathematical concepts, provide multiple solution methods, and explore real-world applications of percentage calculations. Understanding percentages is crucial in various fields, from finance and budgeting to statistics and data analysis. This comprehensive guide will equip you with the knowledge and skills to confidently tackle any percentage problem.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "20 is what percent of 25?". This guide covers multiple methods, real-world applications, and expands on percentage concepts for a thorough understanding.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol % represents "percent," meaning "out of 100" or "per hundred". For example, 50% means 50 out of 100, which can be simplified to ½ or 0.5. Percentages are used to represent proportions or parts of a whole. They provide a standardized way to compare different quantities or values.
Method 1: Using the Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case, "20 is what percent of 25?", we identify:
- Part: 20
- Whole: 25
Plugging these values into the formula:
(20 / 25) x 100% = 0.8 x 100% = 80%
Therefore, 20 is 80% of 25.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
20/25 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
20 * 100 = 25 * x
2000 = 25x
x = 2000 / 25
x = 80
Therefore, x = 80%, confirming our previous result.
Method 3: Decimal Conversion and Multiplication
This method involves converting the percentage to a decimal and then multiplying. To find what percent 20 is of 25, we first express the fraction 20/25 as a decimal:
20 ÷ 25 = 0.8
Then, multiply the decimal by 100% to convert it to a percentage:
0.8 x 100% = 80%
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and across various professional fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage calculations. For instance, understanding compound interest requires a strong grasp of percentages. A 5% annual interest rate on a savings account significantly impacts the growth of your savings over time.
-
Sales and Marketing: Analyzing sales figures, tracking conversion rates, calculating discount percentages for promotions, and assessing the effectiveness of marketing campaigns involve extensive use of percentages. Understanding market share and growth percentages helps businesses strategize effectively.
-
Statistics and Data Analysis: Percentages are essential for presenting and interpreting data. Representing data as percentages allows for easy comparison and visualization. For example, expressing survey results as percentages provides a clear understanding of public opinion.
-
Education: Calculating grades, analyzing test scores, and assessing student performance often involve converting raw scores into percentages.
-
Everyday Life: Calculating tips at restaurants, determining discounts during sales, and understanding nutritional information on food labels all require working with percentages.
Expanding on Percentage Concepts: Finding the Whole or the Part
While the initial question focused on finding the percentage, percentage calculations often involve finding the whole or the part given the percentage and another value. Let's explore these scenarios:
Scenario 1: Finding the Whole
-
Problem: 80% of a number is 20. What is the number?
-
Solution: We can set up an equation:
0.80 * x = 20
x = 20 / 0.80
x = 25
Therefore, the number is 25.
Scenario 2: Finding the Part
-
Problem: What is 25% of 80?
-
Solution: We can directly calculate:
0.25 * 80 = 20
Therefore, 25% of 80 is 20.
Percentage Increase and Decrease
Percentage increase and decrease are common applications in various contexts, especially finance and economics.
Percentage Increase: This is calculated by finding the difference between the new and old values, dividing by the old value, and multiplying by 100%.
Formula: [(New Value - Old Value) / Old Value] x 100%
Example: If a product's price increased from $20 to $25, the percentage increase is:
[(25 - 20) / 20] x 100% = 25%
Percentage Decrease: This is calculated similarly, but the difference is subtracted from the old value.
Formula: [(Old Value - New Value) / Old Value] x 100%
Example: If a product's price decreased from $25 to $20, the percentage decrease is:
[(25 - 20) / 25] x 100% = 20%
Advanced Percentage Problems and Techniques
More complex percentage problems might involve multiple steps or require the use of algebraic equations. For instance, problems involving compound interest, percentage changes over multiple periods, or those embedded within word problems necessitate a deeper understanding of the underlying mathematical principles.
Conclusion: Mastering Percentage Calculations
Understanding percentages is a fundamental skill applicable in diverse aspects of life. This article has provided a thorough explanation of how to solve "20 is what percent of 25?", along with multiple solution methods and examples showcasing real-world applications. Mastering percentage calculations empowers you to confidently handle financial situations, analyze data, and solve various quantitative problems with precision and ease. By grasping the core concepts and practicing different problem types, you can build a solid foundation in percentage calculations and improve your quantitative reasoning skills. Remember that consistent practice and a clear understanding of the underlying principles are key to achieving proficiency in this essential mathematical area.
Latest Posts
Latest Posts
-
How Many Pounds Is One Ton Equal
Jul 10, 2025
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
-
How Many Centimeters Are In A Meter Stick
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.