20 Is What Percent Of 45
Kalali
Apr 12, 2025 · 5 min read
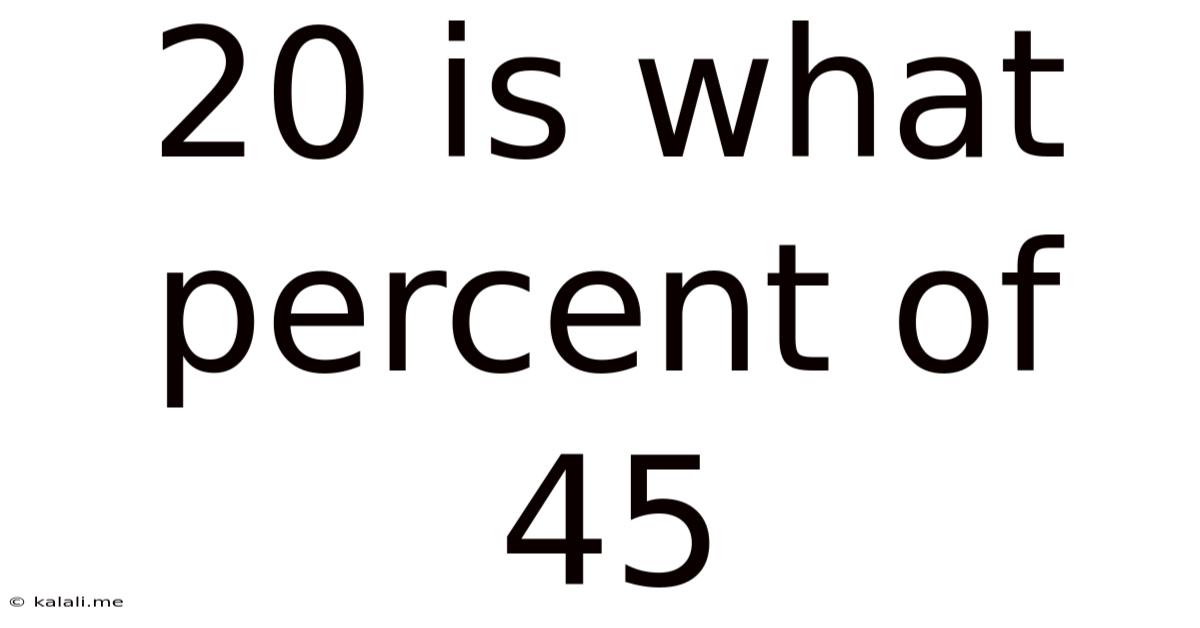
Table of Contents
20 is What Percent of 45? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to solve percentage problems, such as determining what percentage 20 represents of 45, is crucial for navigating these situations effectively. This comprehensive guide will not only answer the question "20 is what percent of 45?" but also delve into the underlying principles, providing you with a robust understanding of percentage calculations and various methods to solve similar problems.
Meta Description: Learn how to calculate percentages with this comprehensive guide. We'll solve the problem "20 is what percent of 45?" and explore different methods for tackling percentage calculations, equipping you with practical skills for various applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, ratios, and rates of change.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "20 is what percent of 45?" is using the fundamental percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 20
- Whole: 45
Substituting these values into the formula, we get:
(20 / 45) * 100 = Percentage
Calculating this:
(0.4444...) * 100 ≈ 44.44%
Therefore, 20 is approximately 44.44% of 45. The slight rounding is due to the recurring decimal in the initial division.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. We can express the problem as a ratio:
20 / 45 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
20 * 100 = 45 * x
2000 = 45x
x = 2000 / 45
x ≈ 44.44%
This method confirms our previous result, demonstrating that 20 is approximately 44.44% of 45.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to obtain the percentage.
- Convert the fraction: Express the problem as a fraction: 20/45
- Simplify the fraction (optional): This step isn't strictly necessary, but simplifying the fraction can make the calculation easier. 20/45 simplifies to 4/9.
- Convert to a decimal: Divide the numerator by the denominator: 4 ÷ 9 ≈ 0.4444...
- Multiply by 100: Multiply the decimal by 100 to express it as a percentage: 0.4444... * 100 ≈ 44.44%
This method again yields the result that 20 is approximately 44.44% of 45.
Understanding the Result and its Implications
The result, approximately 44.44%, signifies that 20 represents roughly 44.44 out of every 100 parts of 45. This understanding can be applied in various real-world scenarios. For example, if 45 represents the total number of students in a class and 20 students passed a particular exam, then approximately 44.44% of the class passed the exam.
Expanding on Percentage Calculations: Practical Applications and Advanced Scenarios
Beyond the basic calculation of "20 is what percent of 45?", understanding percentages extends to various practical applications:
-
Calculating Discounts: Determining the final price of an item after a percentage discount. For example, a 20% discount on a $50 item means a reduction of $10 ($50 * 0.20 = $10), resulting in a final price of $40.
-
Determining Tax Amounts: Calculating the amount of tax payable on a purchase. If the sales tax is 6%, you'd multiply the purchase price by 0.06 to find the tax amount.
-
Calculating Interest: Determining the interest earned on a savings account or the interest payable on a loan. Compound interest calculations involve more complex percentage computations.
-
Analyzing Data and Statistics: Percentages are crucial in presenting and interpreting data, such as in market research, scientific studies, and economic analysis. For instance, representing survey results or changes in population figures often uses percentages.
-
Understanding Growth Rates: Calculating percentage increases or decreases over time, such as population growth, economic growth, or the change in stock prices.
Advanced Percentage Problems: Tackling More Complex Scenarios
While the "20 is what percent of 45?" problem is relatively straightforward, other percentage problems can be more complex. Here are some examples:
-
Finding the Whole: If 30% of a number is 60, what is the number? (Solution: 60 / 0.30 = 200)
-
Finding the Part: What is 15% of 80? (Solution: 80 * 0.15 = 12)
-
Percentage Change: A product's price increased from $25 to $30. What is the percentage increase? (Solution: [(30-25)/25] * 100 = 20%)
-
Successive Percentage Changes: A price increased by 10% and then decreased by 10%. Is the final price the same as the original price? (No, it will be slightly lower due to the compounding effect.)
Mastering these advanced scenarios requires a strong understanding of the underlying principles and the ability to manipulate the percentage formula effectively.
Utilizing Technology for Percentage Calculations
Many tools can simplify percentage calculations, including:
-
Calculators: Most calculators have a percentage function, making calculations quick and easy.
-
Spreadsheets (like Excel or Google Sheets): Spreadsheets offer powerful functions for performing complex percentage calculations and analyzing data.
-
Online Percentage Calculators: Numerous websites offer free online percentage calculators that can handle various percentage-related problems.
Conclusion: Mastering the Art of Percentage Calculations
The ability to solve percentage problems, as demonstrated by calculating that 20 is approximately 44.44% of 45, is a vital skill for various aspects of life. By understanding the fundamental formula, alternative calculation methods, and the diverse applications of percentages, you can confidently tackle a wide range of numerical challenges. Remember to practice regularly to build proficiency and to explore more advanced scenarios to broaden your understanding of this essential mathematical concept. The more you practice, the more intuitive percentage calculations will become, allowing you to apply this knowledge effectively in your personal and professional life.
Latest Posts
Latest Posts
-
Is Liver Cell Haploid Or Diploid
Apr 13, 2025
-
3 Is 40 Percent Of What
Apr 13, 2025
-
How To Find Points Of Intersection Between Two Functions
Apr 13, 2025
-
What Are The Factors For 32
Apr 13, 2025
-
Is Baking A Cake A Physical Change
Apr 13, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.